题目内容
已知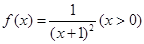 .
.
(1)若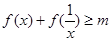 恒成立,求
恒成立,求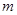 的最大值;
的最大值;
(2)若 为常数,且
为常数,且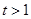 ,记
,记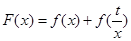 ,求
,求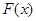 的最小值.
的最小值.
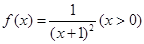 .
.(1)若
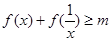 恒成立,求
恒成立,求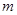 的最大值;
的最大值;(2)若
 为常数,且
为常数,且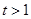 ,记
,记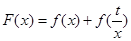 ,求
,求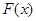 的最小值.
的最小值.(1)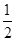 ;(2)
;(2)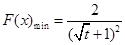 .
.
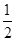 ;(2)
;(2)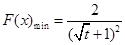 .
.试题分析:本题考查导数与函数及运用导数求单调区间、最值等数学知识,突出考查运用数学知识和方法分析问题解决问题的能力.第一问,是恒成立问题,先将恒成立问题转化为最值问题,求
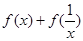 的最值是本问的关键,法一,利用基本不等式求最值,法二,利用导数求最值,无论用哪种方法都应注意函数的定义域;第二问,令
的最值是本问的关键,法一,利用基本不等式求最值,法二,利用导数求最值,无论用哪种方法都应注意函数的定义域;第二问,令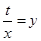 ,将
,将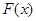 进行转化,化简成
进行转化,化简成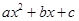 的形式,利用二次函数的单调性求
的形式,利用二次函数的单调性求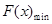 .
.试题解析:(1)(解法一)
设
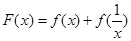
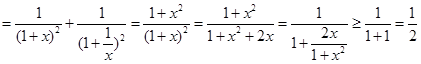 ,
,∴
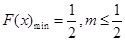 ,∴
,∴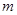 的最大值为
的最大值为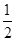 .
.(解法二)设
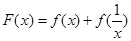
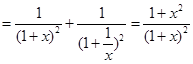 ,
,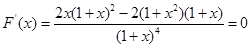 ,
,∴
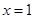 ,当
,当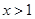 时,
时,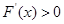 ,当
,当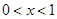 时,
时,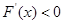 ,∴
,∴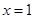 为极小值点,
为极小值点,∴
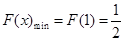 ,∴
,∴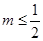 ,∴
,∴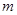 的最大值为
的最大值为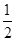 .
.(2)设
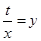 ,则
,则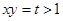 ,则
,则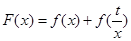
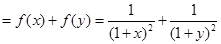
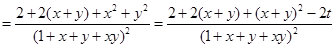

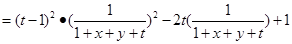
令
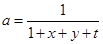 ,则
,则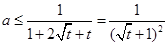
即
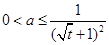 ,
,设
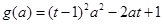 ,∵
,∵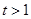 其对称轴
其对称轴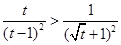 ,
,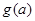 在
在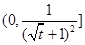 上单调递减,∴
上单调递减,∴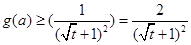 ,
,∴
 ,
,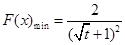 .
.
练习册系列答案
相关题目
 且
且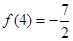 .
.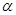 的值;
的值;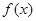 在
在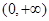 上的单调性,并给予证明.
上的单调性,并给予证明.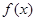 的定义域为
的定义域为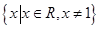 ,且
,且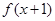 为奇函数,当
为奇函数,当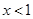 时,
时,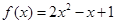 ,那么当
,那么当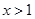 时,
时,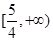
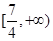
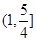
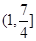
 是偶函数,当
是偶函数,当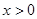 时,其导函数
时,其导函数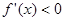 ,则满足
,则满足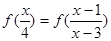 的所有
的所有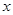 之和为_________.
之和为_________.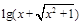 +x,如果f(1-a)+f(1-a2)<0,则a的取值范围是_____
+x,如果f(1-a)+f(1-a2)<0,则a的取值范围是_____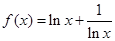 ,则下列结论中正确的是( )
,则下列结论中正确的是( )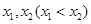 是
是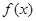 的极值点,则
的极值点,则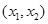 内是增函数
内是增函数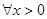 ,且
,且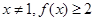
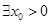 ,
,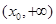 上是增函数
上是增函数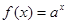 (
( ),数列
),数列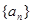 满足
满足 ,
, ,
,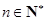 .则
.则 与
与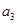 中,较大的是 ;
中,较大的是 ;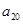 ,
,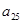 ,
,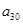 的大小关系是 .
的大小关系是 .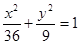 上有两个动点P、Q,E(3,0),EP
上有两个动点P、Q,E(3,0),EP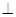 EQ,则
EQ,则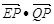 的最小值为( )
的最小值为( )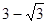
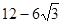
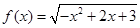 的单调递减区间是 ( )
的单调递减区间是 ( ) 
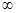 ,-1),(3,+
,-1),(3,+