题目内容
已知函数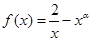 且
且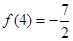 .
.
(1)求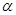 的值;
的值;
(2)判断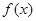 在
在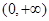 上的单调性,并给予证明.
上的单调性,并给予证明.
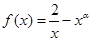 且
且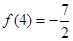 .
.(1)求
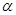 的值;
的值;(2)判断
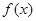 在
在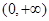 上的单调性,并给予证明.
上的单调性,并给予证明.(1)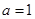 ;(2)
;(2)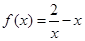 在
在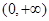 上是减函数.
上是减函数.
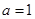 ;(2)
;(2)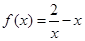 在
在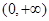 上是减函数.
上是减函数.试题分析:(1)
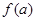 表示函数
表示函数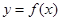 中自变量
中自变量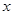 取值为
取值为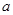 时对应的函数值;(2)函数单调性的证明一般是用单调性的定义证明,即设
时对应的函数值;(2)函数单调性的证明一般是用单调性的定义证明,即设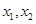 是区间
是区间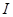 上的任意两个实数,且
上的任意两个实数,且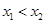 ,然后证明
,然后证明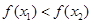 (函数在区间
(函数在区间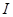 上为为增函数)或
上为为增函数)或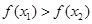 (函数在区间
(函数在区间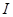 上为减函数).而比较
上为减函数).而比较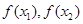 的大小,通常是作差
的大小,通常是作差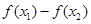 ,然后把差变成若干因式之积,从而很快判断出差的正负.
,然后把差变成若干因式之积,从而很快判断出差的正负.试题解析:解 (1)∵
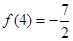 ,∴
,∴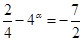 ,
,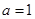 .
.(2)
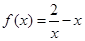 在
在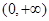 上是减函数.
上是减函数.证明如下:
设任意
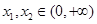 ,且
,且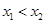 .
.则
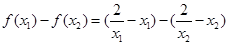
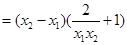 .
.∵
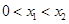 ,∴
,∴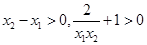 .
.∴
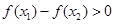 ,即
,即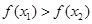 ,
,故
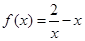 在
在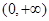 上是减函数.
上是减函数.
练习册系列答案
相关题目
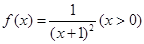 .
.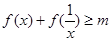 恒成立,求
恒成立,求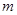 的最大值;
的最大值; 为常数,且
为常数,且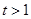 ,记
,记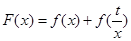 ,求
,求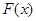 的最小值.
的最小值.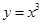
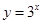
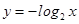
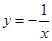
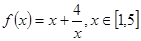 ,则函数
,则函数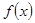 的值域为 .
的值域为 .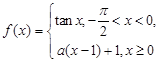 在
在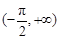 上单调递增,则实数
上单调递增,则实数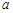 的取值范围( )
的取值范围( )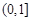
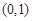
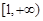
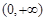
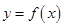 是定义在实数集R上的奇函数,且当
是定义在实数集R上的奇函数,且当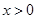 时,
时,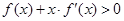 (其中
(其中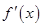 是
是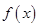 的导函数)恒成立.若
的导函数)恒成立.若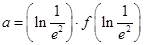 ,
,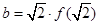 ,
,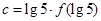 ,则a,b,c的大小关系是( )
,则a,b,c的大小关系是( )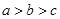

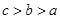
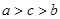
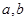 是任意非零常数,对于函数
是任意非零常数,对于函数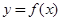 有以下5个命题:
有以下5个命题: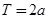 的周期函数的充要条件是
的周期函数的充要条件是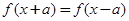 ;
;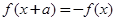 ;
; 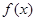 是奇函数且是
是奇函数且是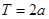 的周期函数,则
的周期函数,则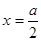 对称;
对称;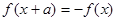 ,则
,则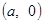 对称,关于直线
对称,关于直线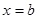 对称,则
对称,则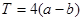 的周期函数.
的周期函数. ,则
,则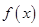 =( )
=( )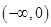 上单调递增
上单调递增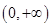 上单调递增
上单调递增