题目内容
1.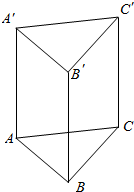 如图,已知$\overrightarrow{AA'}$=$\overrightarrow{BB'}$=$\overrightarrow{CC'}$,求证:
如图,已知$\overrightarrow{AA'}$=$\overrightarrow{BB'}$=$\overrightarrow{CC'}$,求证:(1)△ABC≌△A′B′C′;
(2)$\overrightarrow{AB}$=$\overrightarrow{A'B'}$,$\overrightarrow{AC}$=$\overrightarrow{A'C'}$.
分析 由棱柱的结构特征,可得四边形ABB′A′,四边形ACC′A′,四边形BCC′B′均为平行四边形,进而证得结论.
解答 证明:(1)∵$\overrightarrow{AA'}$=$\overrightarrow{BB'}$=$\overrightarrow{CC'}$,
故四边形ABB′A′,四边形ACC′A′,四边形BCC′B′均为平行四边形,
故AB=A′B′,BC=B′C′,AC=A′C′,
故)△ABC≌△A′B′C′;
(2)由(1)中四边形ABB′A′,四边形ACC′A′,四边形BCC′B′均为平行四边形,
可得向量$\overrightarrow{AB}$与$\overrightarrow{A'B'}$方向相同,大小相等,
故$\overrightarrow{AB}$=$\overrightarrow{A'B'}$,
同理$\overrightarrow{AC}$=$\overrightarrow{A'C'}$.
点评 本题考查的知识点是棱柱的结构特征,平行四边形的判定与性质,向量相等,难度中档.

练习册系列答案
相关题目
9.设x∈R,则“|x-2|<1”是“x2+x>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
6.为了了解市民的环保意识,某校高一(1)班50名学生在6月5日(世界环境日)这一天调查了各自家庭丢弃旧塑料袋的情况,有关数据如下表:
(1)求这50户居民每天丢弃旧塑料袋的平均数;
(2)求这50户居民每天丢弃旧塑料袋的方差.
| 每户丢弃旧塑料袋个数 | 2 | 3 | 4 | 5 |
| 户数 | 10 | 10 | 20 | 10 |
(2)求这50户居民每天丢弃旧塑料袋的方差.
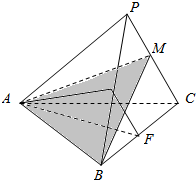 在三棱锥P-ABC中,AP=AC,BP=BC,E、F、M分别是PB、BC、CP的中点,求证:平面AEF⊥平面ABM.
在三棱锥P-ABC中,AP=AC,BP=BC,E、F、M分别是PB、BC、CP的中点,求证:平面AEF⊥平面ABM.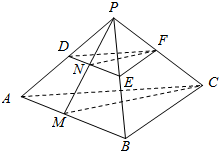 如图,在三棱锥P-ABC中,D,E,F分别是PA,PB,PC的中点.M是AB上一点,连接MC,N是PM与DE的交点,连接NF,求证:NF∥CM.
如图,在三棱锥P-ABC中,D,E,F分别是PA,PB,PC的中点.M是AB上一点,连接MC,N是PM与DE的交点,连接NF,求证:NF∥CM.