题目内容
【题目】已知函数f（x）=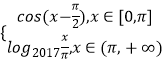 
，若有三个不同的实数a，b，c，使得f（a）=f（b）=f（c），则a+b+c的取值范围为（ ）
A.（2π，2017π）
B.（2π，2018π）
C.（ 
， 
）
D.（π，2017π）
【答案】B
【解析】解：当x∈[0，π]时，f（x）=cos（x﹣ 
）=sinx， ∴f（x）在[0，π]上关于x= 对称，且fmax（x）=1，
又当x∈（π，+∞）时，f（x）=log2017 
是增函数，
作出y=f（x）的函数图象如图所示：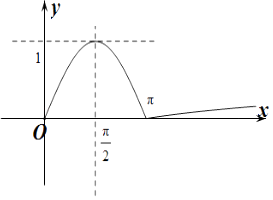
令log2017 =1得x=2017π，
∵f（a）=f（b）=f（c），
∴a+b=π，c∈（π，2017π），
∴a+b+c=π+c∈（2π，2018π）．
故选：B．
【题目】随着南宁三中集团化发展，南宁三中青三校区2018年被清华北大录取23人，广西领先，一本率连年攀升，南宁三中青山校区2014年至2018年一本率如下表：
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
时间代号 | 1 | 2 | 3 | 4 | 5 |
一本率 | 0.7152 | 0.7605 | 0.7760 | 0.8517 | 0.9015 |
(1)求
关于
的回归方程
(精确到0.0001);
(2)用所求回归方程预测南宁三中青山校区2019年高考一本录取率.(精确到0.0001).
附：回归方程中
参考数据：
【题目】理科竞赛小组有9名女生、12名男生，从中随机抽取一个容量为7的样本进行分析．
（Ⅰ）如果按照性别比例分层抽样，可以得到多少个不同的样本？（写出算式即可）
（Ⅱ）如果随机抽取的7名同学的物理、化学成绩（单位：分）对应如表：
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
物理成绩 | 65 | 70 | 75 | 81 | 85 | 87 | 93 |
化学成绩 | 72 | 68 | 80 | 85 | 90 | 86 | 91 |
规定85分以上（包括85份）为优秀，从这7名同学中再抽取3名同学，记这3名同学中物理和化学成绩均为优秀的人数为X，求随机变量X的分布列和数学期望．
【题目】2017年春晚分会场之一是凉山西昌，电视播出后，通过网络对凉山分会场的表演进行了调查．调查分三类人群进行，参加了网络调查的观众们的看法情况如下：
观众对凉山分会场表演的看法 | 非常好 | 好 |
中国人且非四川（人数比例） |
|
|
四川人（非凉山）（人数比例） |
|
|
凉山人（人数比例） |
|
|
（1）从这三类人群中各选一个人，求恰好有2人认为“非常好”的概率（用比例作为相应概率）；
（2）若在四川人（非凉山）群中按所持态度分层抽样，抽取9人，在这9人中任意选取3人，认为“非常好”的人数记为ξ，求ξ的分布列和数学期望．