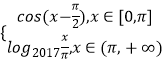题目内容
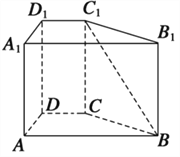
【题目】右图是一个几何体的平面展开图，其中ABCD为
正方形， E、F分别为PA、PD的中点，在此几何体中，
给出下面四个结论：
①直线BE与直线CF异面；②直线BE与直线AF异面；
③直线EF//平面PBC； ④平面BCE⊥平面PAD.
其中正确结论的个数是
A. 1个 B. 2个 C. 3个 D. 4个
【答案】2个
【解析】
①连接EF，由E、F分别为PA、PD的中点，可得EF∥AD，从而可得E，F，B，C共面，故直线BE与直线CF是共面直线；
②根据E∈平面PAD，AF平面PAD，EAF，B平面PAD，可得直线BE与直线AF是异面直线；
③由①知EF∥BC，利用线面平行的判定可得直线EF∥平面PBC；
④由于不能推出线面垂直，故平面BCE⊥平面PAD不成立．
解：如图所示，
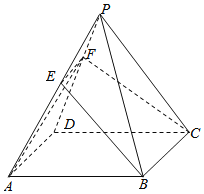
①连接EF，则∵E、F分别为PA、PD的中点，∴EF∥AD，∵AD∥BC，∴EF∥BC，∴E，F，B，C共面，∴直线BE与直线CF是共面直线，故①正确；
②∵E∈平面PAD，AF平面PAD，EAF，B平面PAD，∴直线BE与直线AF是异面直线，故②正确；
③由①知EF∥BC，∵EF平面PBC，BC平面PBC，∴直线EF∥平面PBC，故③正确；
④由于不能推出线面垂直，故平面BCE⊥平面PAD不成立．
故选：B．
练习册系列答案
名校课堂系列答案
相关题目
