题目内容
【题目】已知直线![]() 经过直线
经过直线![]() 与
与![]() 的交点
的交点![]() .
.
(1)点![]() 到直线
到直线![]() 的距离为3,求直线
的距离为3,求直线![]() 的方程;
的方程;
(2)求点![]() 到直线
到直线![]() 的距离的最大值,并求距离最大时的直线
的距离的最大值,并求距离最大时的直线![]() 的方程.
的方程.
【答案】(1) x=2或4x-3y-5=0(2)见解析.
【解析】试题分析:(1)设过两直线的交点的直线系方程,再根据点到直线的距离公式,求出![]() 的值,得出直线
的值,得出直线![]() 的方程;(2)先求出交点P的坐标,由几何的方法求出距离的最大值。
的方程;(2)先求出交点P的坐标,由几何的方法求出距离的最大值。
试题解析:(1)因为经过两已知直线交点的直线系方程为
(2x+y-5)+λ(x-2y)=0,即(2+λ)x+(1-2λ)y-5=0,
所以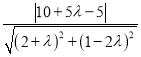 =3,解得λ=
=3,解得λ=![]() 或λ=2
或λ=2
所以直线l的方程为x=2或4x-3y-5=0.
(2)由![]() 解得交点P(2,1),
解得交点P(2,1),
如图,过P作任一直线l,设d为点A到直线l的距离,
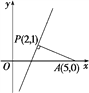
则d≤|PA|(当l⊥PA时等号成立)
所以dmax=|PA|=![]()
此时直线l的方程为: 3x-y-5=0.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目