Question

【题目】已知函数

（1）试用“五点法”画出函数在区间的简图；

（2）指出该函数的图象可由的图象经过怎样的平移和伸缩变换得到？

（3）若时，函数的最小值为，试求出函数的最大值并指出取何值时，函数取得最大值．

Answer 1

【答案】（1）图见解析；（2）见解析；（3）当时，最大值为

【解析】

（1）利用五点法，即将看成整体取正弦函数的五个关键点，通过列表、描点、连线

画出函数图象；（2）用图象变换的方法得此函数图象，可以先向左平移，再横向伸缩，再向上平移的顺序进行；（3），，，求此函数的最值可先将看成整体，求正弦函数的值域，最后利用函数的最小值为2，解方程可得的值，进而求出函数最大值．

（1）先列表，再描点连线，可得简图．

	0
	0	1	0		0

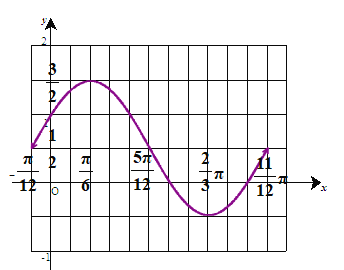
（2）向左平移得到，

再保持纵坐标不变，横坐标缩短为原为的变为，

最后再向上平移个单位得到．

（3），

，，

，，

，，

，，

，

，当即时最大，最大值为．