题目内容
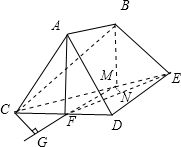
 如图,已知多面体ABCDE中,AB⊥平面ACD,DE∥AB,△ACD是边长为2的正三角形,且DE=2AB=2,F是CD的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE∥AB,△ACD是边长为2的正三角形,且DE=2AB=2,F是CD的中点.(1)求证:AF∥平面BCE;
(2)求面ABC与面EDC所成的二面角的大小(只求其中锐角);
(3)求BE与平面AFE所成角的大小.
分析:(1)取CE的中点为M,则FM∥
DE,并且FM=
DE,结合题意可得:AB∥FM,并且AB=FM,即得到ABMF为平行四边形,所以AF∥BM,进而结合线面平行的判定定理得到线面平行.
(2)过点C作直线l∥AB,则l∥DE,可得平面ABC∩平面CDE=l,结合题意可得:l⊥平面ACD,再由二面角的定义可得:∠ACD即为所求二面角的平面角,进而利用解三角形的有关知识得到答案.
(3)设B在平面AFE内的射影为B′,作MN⊥FE于N,作CG⊥EF于G,得到BE与平面AFE所成角即为∠BEB′,再把线面角放入直角三角形中,进而利用解三角形的有关知识求出线面角.
| 1 |
| 2 |
| 1 |
| 2 |
(2)过点C作直线l∥AB,则l∥DE,可得平面ABC∩平面CDE=l,结合题意可得:l⊥平面ACD,再由二面角的定义可得:∠ACD即为所求二面角的平面角,进而利用解三角形的有关知识得到答案.
(3)设B在平面AFE内的射影为B′,作MN⊥FE于N,作CG⊥EF于G,得到BE与平面AFE所成角即为∠BEB′,再把线面角放入直角三角形中,进而利用解三角形的有关知识求出线面角.
解答:解:(1)证明:取CE的中点为M,则FM∥
DE,并且FM=
DE,
由题意可得:AB∥
DE,并且AB=
DE,
所以AB∥FM,并且AB=FM,
所以ABMF为平行四边形,
所以AF∥BM,
又因为AF?平面BCE,BM?平面BCE,
所以AF∥平面BCE.
(2)过点C作直线l∥AB,则l∥DE,
所以平面ABC∩平面CDE=l,
因为AB⊥平面ACD,
所以l⊥平面ACD,
所以AC⊥l,CD⊥l,
所以∠ACD即为所求二面角的平面角.
又因为,△ACD是边长为2的正三角形,
所以∠ACD=60°,即面ABC与面EDC所成的二面角的大小为60°.
(3)设B在平面AFE内的射影为B′,作MN⊥FE于N,作CG⊥EF于G,
所以BE与平面AFE所成角即为∠BEB′,
因为AF⊥CD,AF⊥DE,
所以AF⊥平面CDE,所以AF⊥MN,
又因为MN⊥FE,AF∩EF=F,并且AF?平面AEF,EF?平面AEF,
所以MN⊥平面AEF.
因为BM∥平面AEF,
所以BB′=MN,
由△CGF∽△EDF可得:CG=
,所以MN=
CG=
,
因为BE=
,
所以sin∠BEB′=
=
,
所以∠BEB′=arcsin
.
| 1 |
| 2 |
| 1 |
| 2 |
由题意可得:AB∥
| 1 |
| 2 |
| 1 |
| 2 |
所以AB∥FM,并且AB=FM,
所以ABMF为平行四边形,
所以AF∥BM,
又因为AF?平面BCE,BM?平面BCE,
所以AF∥平面BCE.
(2)过点C作直线l∥AB,则l∥DE,

所以平面ABC∩平面CDE=l,
因为AB⊥平面ACD,
所以l⊥平面ACD,
所以AC⊥l,CD⊥l,
所以∠ACD即为所求二面角的平面角.
又因为,△ACD是边长为2的正三角形,
所以∠ACD=60°,即面ABC与面EDC所成的二面角的大小为60°.
(3)设B在平面AFE内的射影为B′,作MN⊥FE于N,作CG⊥EF于G,
所以BE与平面AFE所成角即为∠BEB′,
因为AF⊥CD,AF⊥DE,
所以AF⊥平面CDE,所以AF⊥MN,
又因为MN⊥FE,AF∩EF=F,并且AF?平面AEF,EF?平面AEF,
所以MN⊥平面AEF.
因为BM∥平面AEF,
所以BB′=MN,
由△CGF∽△EDF可得:CG=
| 2 | ||
|
| 1 |
| 2 |
| 1 | ||
|
因为BE=
| 5 |
所以sin∠BEB′=
| BB′ |
| BE |
| 1 |
| 5 |
所以∠BEB′=arcsin
| 1 |
| 5 |
点评:本题主要考查利用线面平行的判定定理证明线面平行,以及求二面角的平面角与线面角的有关知识,而空间角解决的关键是做角,由图形的结构及题设条件正确作出平面角来,是求角的关键,解决空间角也可以根据几何体的结构特征建立空间直角坐标系利用向量的有关知识解决空间角.

练习册系列答案
相关题目
 如图,已知多面体ABCDEF中,AB⊥平面ACDF,DE⊥平面ACDF,△ACD是正三角形,且
如图,已知多面体ABCDEF中,AB⊥平面ACDF,DE⊥平面ACDF,△ACD是正三角形,且 如图,已知多面体ABCDE中,DE⊥平面DBC,DE∥AB,BD=CD=BC=AB=2,F为BC的中点.
如图,已知多面体ABCDE中,DE⊥平面DBC,DE∥AB,BD=CD=BC=AB=2,F为BC的中点. 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1. 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点. 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.