题目内容
【题目】记![]() 表示m,n中的最大值,如
表示m,n中的最大值,如![]() .已知函数
.已知函数![]() ,
,![]() .
.
(1)设![]() ,求函数
,求函数![]() 在
在![]() 上的零点个数;
上的零点个数;
(2)试探讨是否存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立?若存在,求a的取值范围;若不存在,说明理由.
恒成立?若存在,求a的取值范围;若不存在,说明理由.
【答案】(1)2;(2)存在,![]() .
.
【解析】
(1)利用导数求出![]() 的单调区间及最值,结合图像即可判定;(2)构造函数
的单调区间及最值,结合图像即可判定;(2)构造函数![]() ,对该函数在
,对该函数在![]() 的最大值进行分类讨论求解,只需要最大值小于0即可.
的最大值进行分类讨论求解,只需要最大值小于0即可.
(1)设![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
所![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]() .
.
设![]() ,结合
,结合![]() 与
与![]() 在
在![]() 上的图象可知,
上的图象可知,
这两个函数的图象在![]() 内有两个交点,
内有两个交点,
即![]() 在
在![]() 上的零点个数为2(或由方程
上的零点个数为2(或由方程![]() 在
在![]() 内有两根可得).
内有两根可得).
(2)假设存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立,
恒成立,
则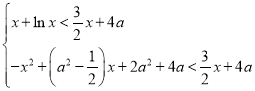 对
对![]() 恒成立,
恒成立,
即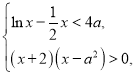 对
对![]() 恒成立,
恒成立,
①设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
所以![]() ,
,
当![]() 即
即![]() 时,
时,![]() ,所以
,所以![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
故当![]() 时,
时,![]() 对
对![]() 恒成立;
恒成立;
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上递减,
上递减,
所以![]() .
.
因为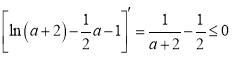 ,所以
,所以![]() ,
,
故当![]() 时,
时,![]() 对
对![]() 恒成立.
恒成立.
②若![]() 对
对![]() 恒成立,
恒成立,
则![]() ,
,
所以![]() .
.
由①②得,![]() .
.
故存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立,且a的取值范围为
恒成立,且a的取值范围为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】2018年11月5日至10日,首届中国国际进口博览会在国家会展中心(上海)举行,吸引了58个“一带一路”沿线国家的超过1000多家企业参展,成为共建“一带一路”的又一个重要支撑.某企业为了参加这次盛会,提升行业竞争力,加大了科技投入.该企业连续6年来的科技投入![]() (百万元)与收益
(百万元)与收益![]() (百万元)的数据统计如下:
(百万元)的数据统计如下:
科技投入 | 2 | 4 | 6 | 8 | 10 | 12 |
收益 | 5.6 | 6.5 | 12.0 | 27.5 | 80.0 | 129.2 |
并根据数据绘制散点图如图所示:
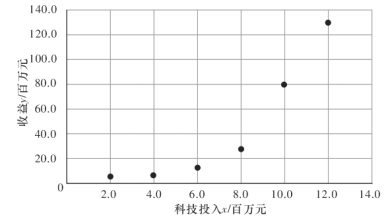
根据散点图的特点,甲认为样本点分布在指数曲线![]() 的周围,据此他对数据进行了一些初步处理.如下表:
的周围,据此他对数据进行了一些初步处理.如下表:
|
|
|
|
|
|
43.5 | 4.5 | 854.0 | 34.7 | 12730.4 | 70 |
其中![]() ,
,![]() .
.
(1)(i)请根据表中数据,建立![]() 关于
关于![]() 的回归方程(保留一位小数);
的回归方程(保留一位小数);
(ii)根据所建立的回归方程,若该企业想在下一年收益达到2亿,则科技投入的费用至少要多少?(其中![]() )
)
(2)乙认为样本点分布在二次曲线![]() 的周围,并计算得回归方程为
的周围,并计算得回归方程为![]() ,以及该回归模型的相关指数
,以及该回归模型的相关指数![]() ,试比较甲乙两人所建立的模型,谁的拟合效果更好.
,试比较甲乙两人所建立的模型,谁的拟合效果更好.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线方程
,其回归直线方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为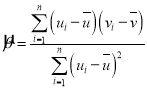 ,
,![]() ,相关指数:
,相关指数: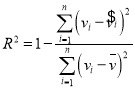 .
.