题目内容
(本题满分16分)
已知圆![]()
![]() ,相互垂直的两条直线
,相互垂直的两条直线![]() 、
、![]() 都过点
都过点![]() .
.
(Ⅰ)当![]() 时,若圆心为
时,若圆心为![]() 的圆和圆
的圆和圆![]() 外切且与直线
外切且与直线![]() 、
、![]() 都相切,求圆
都相切,求圆![]() 的方程;
的方程;
(Ⅱ)当![]() 时,求
时,求![]() 、
、![]() 被圆
被圆![]() 所截得弦长之和的最大值,并求此时直线
所截得弦长之和的最大值,并求此时直线![]() 的方程.
的方程.
解:(Ⅰ)设圆![]() 的半径为
的半径为![]() ,易知圆心
,易知圆心![]() 到点
到点![]() 的距离为
的距离为![]() ,
,
∴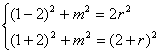 , ………………………………4分
, ………………………………4分
解得![]() 且
且![]() ∴圆
∴圆![]() 的方程为
的方程为![]() . ……………7分
. ……………7分
(Ⅱ)当![]() 时,设圆
时,设圆![]() 的圆心为
的圆心为![]() ,
,![]() 、
、![]() 被圆
被圆![]() 所截得弦的中点分别为
所截得弦的中点分别为![]() ,弦长分别为
,弦长分别为![]() ,因为四边形
,因为四边形![]() 是矩形,所以
是矩形,所以![]() ,即
,即
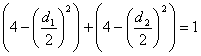 ,化简得
,化简得![]() . ……………………10分
. ……………………10分
从而![]() ,
,
∴![]() ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
∴当![]() 时,有
时,有![]() ,
,
即![]() 、
、![]() 被圆
被圆![]() 所截得弦长之和的最大值为
所截得弦长之和的最大值为![]() . ……………13分
. ……………13分
此时![]() ,显然直线
,显然直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为:
的方程为:![]() ,
,
则![]() ,
,![]() . …………………………15分
. …………………………15分
∴直线![]() 的方程为:
的方程为:![]() 或
或![]() . …………………………16分
. …………………………16分

练习册系列答案
 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目


 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在