题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且椭圆
,且椭圆![]() 的右顶点到直线
的右顶点到直线![]() 的距离为3.
的距离为3.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的面积的最大值(
的面积的最大值(![]() 为坐标原点).
为坐标原点).
【答案】(1)![]() .(2)
.(2)![]()
【解析】
(1)根据椭圆![]() 的右顶点到直线
的右顶点到直线![]() 的距离为3可求
的距离为3可求![]() ,然后利用离心率可求
,然后利用离心率可求![]() ,结合
,结合![]() 的关系可得椭圆的方程;
的关系可得椭圆的方程;
(2)设出直线方程,联立椭圆方程,结合韦达定理可求![]() ,结合三角形面积公式及基本不等式可求
,结合三角形面积公式及基本不等式可求![]() 的面积的最大值.
的面积的最大值.
(1)因为椭圆![]() 的右顶点到直线
的右顶点到直线![]() 的距离为3,
的距离为3,
所以 ,解得
,解得![]() 或
或![]() (舍).
(舍).
因为椭圆![]() 的离心率为
的离心率为![]() ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]() .
.
故椭圆![]() 的方程为
的方程为![]() .
.
(2)由题意可知直线![]() 的斜率不为0,
的斜率不为0,
则可设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() ,
,
联立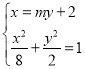 ,整理得
,整理得![]() ,
,
则![]() ,
,![]() ,
,
从而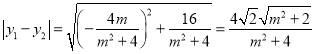 .
.
故![]() 的面积
的面积![]() .
.
设![]() ,则
,则![]() ,故
,故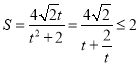 ,
,
当且仅当![]() ,即
,即![]() 时,
时,![]() 的面积取得最大值2.
的面积取得最大值2.

练习册系列答案
相关题目
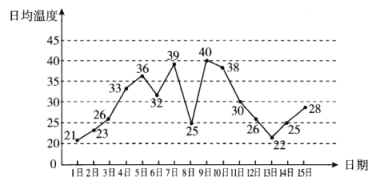
【题目】某快餐连锁店,每天以200元的价格从总店购进早餐,然后以每份10元的价格出售.40份以内,总店收成本价每份5元,当天不能出售的早餐立即以1元的价格被总店回收,超过40份的未销售的部分总店成本价回收,然后进行环保处理.如果销售超过40份,则超过40份的利润需上缴总店.该快餐连锁店记录了100天早餐的销售量(单位:份),整理得下表:
日销售量 | 25 | 30 | 35 | 40 | 45 | 50 |
频数 | 10 | 16 | 28 | 24 | 14 | 8 |
完成下列问题:
(1)写出每天获得利润![]() 与销售早餐份数
与销售早餐份数![]() (
(![]() )的函数关系式;
)的函数关系式;
(2)估计每天利润不低于150元的概率;
(3)估计该快餐店每天的平均利润.