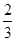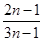题目内容
已知首项为正数的等差数列{an}的前n项和为Sn,若a1 006和a1 007是方程x2-2 012x-2 011=0的两根,则使Sn>0成立的正整数n的最大值是________.
2011
由题意知,a1 006+a1 007=2 012>0,a1 006·a1 007=-2 011<0,又因首项为正等差数列,所以a1 006>0,a1 007<0,2a1 006=a1+a2 011>0,2a1 007=a1+a2 013<0,即S2 011>0,S2 013<0,又因Sn= ,n的最大值为2011.
,n的最大值为2011.
 ,n的最大值为2011.
,n的最大值为2011.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
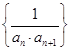 的前100项和为 ( ).
的前100项和为 ( ).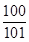
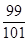


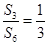 ,则
,则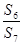 =________.
=________.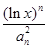 ,若对任意的实数x∈(1,e](e是自然对数的底)和任意正整数n,总有Tn<r(r∈N+).则r的最小值为________.
,若对任意的实数x∈(1,e](e是自然对数的底)和任意正整数n,总有Tn<r(r∈N+).则r的最小值为________.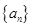 ,
,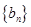 的前
的前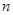 项和分别为
项和分别为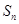 ,
,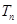 ,若
,若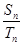
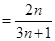 ,则
,则 ( )
( )