题目内容
设数列{an}的各项均为正数,前n项和为Sn,对于任意的n∈N+,an,Sn,a成等差数列,设数列{bn}的前n项和为Tn,且bn=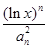 ,若对任意的实数x∈(1,e](e是自然对数的底)和任意正整数n,总有Tn<r(r∈N+).则r的最小值为________.
,若对任意的实数x∈(1,e](e是自然对数的底)和任意正整数n,总有Tn<r(r∈N+).则r的最小值为________.
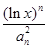 ,若对任意的实数x∈(1,e](e是自然对数的底)和任意正整数n,总有Tn<r(r∈N+).则r的最小值为________.
,若对任意的实数x∈(1,e](e是自然对数的底)和任意正整数n,总有Tn<r(r∈N+).则r的最小值为________.2
根据题意,对于任意n∈N+,总有an,Sn,a成等差数列,则对于n∈N*,总有2Sn=an+ ①
①
所以2Sn-1=an-1+ (n≥2)②
(n≥2)②
①-②得2an=an+ -an-1-
-an-1- ,即an+an-1=(an+an-1)(an-an-1)因为an,an-1均为正数,所以an-an-1=1(n≥2),
,即an+an-1=(an+an-1)(an-an-1)因为an,an-1均为正数,所以an-an-1=1(n≥2),
所以数列{an}是公差为1的等差数列,又n=1时,2S1=a1+a,解得a1=1,所以an=n,对于任意的实数x∈(1,e],有0<ln x<1,对于任意正整数n.总有bn=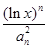 ≤
≤ ,所以Tn≤
,所以Tn≤ =
= ,又对任意的实数x∈(1,e]和任意正整数n,总有Tn<r(r∈N+),所以r的最小值为2.
,又对任意的实数x∈(1,e]和任意正整数n,总有Tn<r(r∈N+),所以r的最小值为2.
 ①
①所以2Sn-1=an-1+
 (n≥2)②
(n≥2)②①-②得2an=an+
 -an-1-
-an-1- ,即an+an-1=(an+an-1)(an-an-1)因为an,an-1均为正数,所以an-an-1=1(n≥2),
,即an+an-1=(an+an-1)(an-an-1)因为an,an-1均为正数,所以an-an-1=1(n≥2),所以数列{an}是公差为1的等差数列,又n=1时,2S1=a1+a,解得a1=1,所以an=n,对于任意的实数x∈(1,e],有0<ln x<1,对于任意正整数n.总有bn=
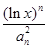 ≤
≤ ,所以Tn≤
,所以Tn≤ =
= ,又对任意的实数x∈(1,e]和任意正整数n,总有Tn<r(r∈N+),所以r的最小值为2.
,又对任意的实数x∈(1,e]和任意正整数n,总有Tn<r(r∈N+),所以r的最小值为2.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
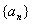 的首项
的首项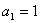 ,前
,前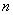 项和为
项和为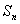 (
(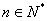 ),且点
),且点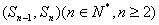 在直线
在直线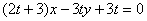 上(
上(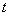 为与
为与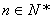 )为等比数列;
)为等比数列;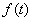 ,数列
,数列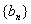 满足
满足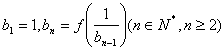 ,设
,设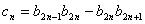 ,求数列
,求数列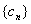 的前
的前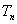 ;
;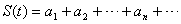 ,求函数
,求函数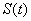 的值域.
的值域.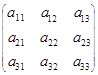 中,每行的3个数依次成等差数列,每列的3个数也依次成等差数列,若
中,每行的3个数依次成等差数列,每列的3个数也依次成等差数列,若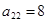 ,则这9个数的和为( )
,则这9个数的和为( )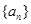 满足:当
满足:当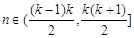 (
(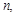
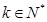 )时,
)时,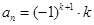 ,
,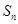 是数列
是数列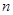 项和,定义集合
项和,定义集合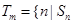 是
是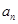 的整数倍,
的整数倍,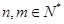 ,且
,且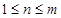
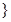 ,
,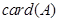 表示集合
表示集合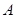 中元素的个数,则
中元素的个数,则 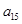 = ,
= , 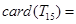 .
.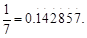 令
令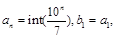 令当n>1时,
令当n>1时,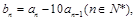 则
则 ,
,  .
.