题目内容
已知函数y=f(x)是偶函数,当x>0时,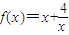 ;当x∈[-3,-1]时,记f(x)的最大值为m,最小值为n,则m-n= .
;当x∈[-3,-1]时,记f(x)的最大值为m,最小值为n,则m-n= .
【答案】分析:先利用偶函数的定义:f(-x)=f(x),结合当x>0时,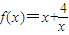 的解析式,求出函数在[-3,-1]上的解析式,再利用导数求出函数的最值即得m-n.
的解析式,求出函数在[-3,-1]上的解析式,再利用导数求出函数的最值即得m-n.
解答:解:当x∈[-3,-1]时,-x∈[1,3]
∵当x>0时,f(x)=
∴f(-x)=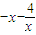
∵函数y=f(x)是偶函数
∴f(x)=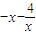 ,x∈[-3,-1]
,x∈[-3,-1]
∵f′(x)=-1+ =
=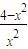
当-3≤x<-2时,f′(x)<0,函数在[-3,-2)上是减函数;当-2<x<-1时,f′(x)>0,函数在[-2,-1]上是增函数,
所以当x=-2时,函数有最小值4;当x=-3时f(-3)=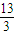 ;
;
当x=-1时,f(-1)=5所以函数的最大值为5
所以m=5,n=4,
故m-n=1,
故答案为1.
点评:本题考查偶函数的定义、函数单调性的应用、函数奇偶性的应用等基础知识,考查运算求解能力,化归与转化思想.属于基础题.
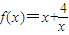 的解析式,求出函数在[-3,-1]上的解析式,再利用导数求出函数的最值即得m-n.
的解析式,求出函数在[-3,-1]上的解析式,再利用导数求出函数的最值即得m-n.解答:解:当x∈[-3,-1]时,-x∈[1,3]
∵当x>0时,f(x)=

∴f(-x)=
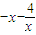
∵函数y=f(x)是偶函数
∴f(x)=
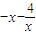 ,x∈[-3,-1]
,x∈[-3,-1]∵f′(x)=-1+
 =
=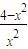
当-3≤x<-2时,f′(x)<0,函数在[-3,-2)上是减函数;当-2<x<-1时,f′(x)>0,函数在[-2,-1]上是增函数,
所以当x=-2时,函数有最小值4;当x=-3时f(-3)=
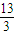 ;
;当x=-1时,f(-1)=5所以函数的最大值为5
所以m=5,n=4,
故m-n=1,
故答案为1.
点评:本题考查偶函数的定义、函数单调性的应用、函数奇偶性的应用等基础知识,考查运算求解能力,化归与转化思想.属于基础题.

练习册系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足