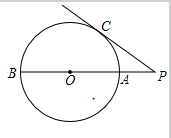
题目内容
在极坐标系中,已知点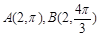 ,C是曲线
,C是曲线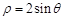 上任意一点,则
上任意一点,则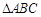 的面积的最小值等于 .
的面积的最小值等于 .
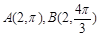 ,C是曲线
,C是曲线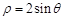 上任意一点,则
上任意一点,则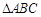 的面积的最小值等于 .
的面积的最小值等于 .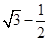
解:A (-2,0 ),B(-1,- 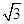 ),曲线ρ=2sinθ 即 ρ2=2ρsinθ,
),曲线ρ=2sinθ 即 ρ2=2ρsinθ,
即 (y-1)2+x2=1,
表示以(0,1)为圆心,以1为半径的圆.
直线AB的方程为即 y=-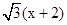 ,
,
圆心到直线AB的距离等于d=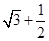 ,故圆上的点到直线AB的距离的最小值等于
,故圆上的点到直线AB的距离的最小值等于 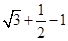
则△ABC的面积的最小值等于 1/ 2 ×2×(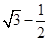 )=
)=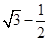 ,
,
故答案为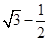
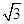 ),曲线ρ=2sinθ 即 ρ2=2ρsinθ,
),曲线ρ=2sinθ 即 ρ2=2ρsinθ,即 (y-1)2+x2=1,
表示以(0,1)为圆心,以1为半径的圆.
直线AB的方程为即 y=-
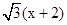 ,
,圆心到直线AB的距离等于d=
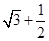 ,故圆上的点到直线AB的距离的最小值等于
,故圆上的点到直线AB的距离的最小值等于 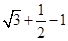
则△ABC的面积的最小值等于 1/ 2 ×2×(
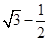 )=
)=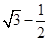 ,
,故答案为

练习册系列答案
相关题目
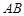 是圆
是圆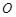 的直径,
的直径,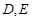 为圆上位于
为圆上位于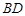 并延长至点
并延长至点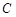 ,使
,使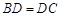 ,连结
,连结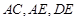 .
.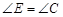 .
.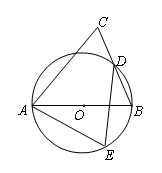
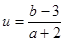 的最大值为__________.
的最大值为__________.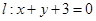 和圆
和圆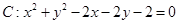 ,设A是直线
,设A是直线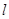 上动点,直线AC交圆于点B,若在圆C上存在点M,使
上动点,直线AC交圆于点B,若在圆C上存在点M,使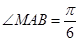 ,则点A的横坐标的取值范围为 。
,则点A的横坐标的取值范围为 。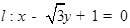 ,一个圆的圆心
,一个圆的圆心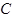 在
在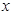 轴正半轴上,且该圆与直线
轴正半轴上,且该圆与直线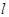 和
和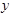 轴均相切.
轴均相切.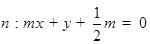 与圆
与圆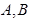 两点,且
两点,且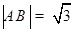 ,求
,求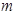 的值.
的值.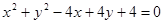 上有四点到直线
上有四点到直线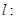
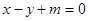 的距离为
的距离为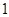 ,则
,则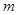 的取值范围为______________.
的取值范围为______________.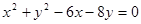 ,过坐标原点作长为8的弦,求弦所在直线的方程.
,过坐标原点作长为8的弦,求弦所在直线的方程.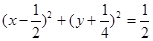 的切线,则此切线长为
的切线,则此切线长为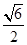
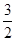
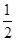
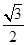
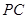 切圆
切圆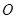 于点
于点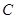 ,割线
,割线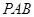 经过圆心
经过圆心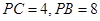 ,则
,则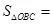 .
.