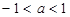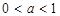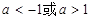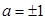题目内容
(本小题满分12分)圆的方程为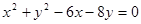 ,过坐标原点作长为8的弦,求弦所在直线的方程.
,过坐标原点作长为8的弦,求弦所在直线的方程.
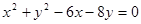 ,过坐标原点作长为8的弦,求弦所在直线的方程.
,过坐标原点作长为8的弦,求弦所在直线的方程.x2+y2-6x-8y=0即(x-3)2+(y-4)2=25,
若直线有斜率,则设所求直线为y=kx.…………2分
∵圆半径为5,
∴圆心M(3,4)到该直线距离为3,…………4分
∴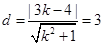 ,…………6分
,…………6分
∴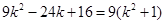 ,∴
,∴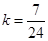 . …………8分
. …………8分
∴所求直线为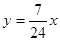 …………9分
…………9分
若直线没有斜率,即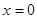 ,直线与圆两交点分别是A(0,0)、B(0,8),
,直线与圆两交点分别是A(0,0)、B(0,8),
弦长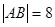 ,…………11分
,…………11分
综上,弦所在直线方程为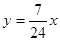 或
或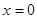 …………12分
…………12分
若直线有斜率,则设所求直线为y=kx.…………2分
∵圆半径为5,
∴圆心M(3,4)到该直线距离为3,…………4分
∴
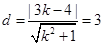 ,…………6分
,…………6分 ∴
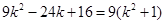 ,∴
,∴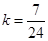 . …………8分
. …………8分 ∴所求直线为
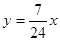 …………9分
…………9分 若直线没有斜率,即
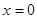 ,直线与圆两交点分别是A(0,0)、B(0,8),
,直线与圆两交点分别是A(0,0)、B(0,8),弦长
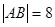 ,…………11分
,…………11分 综上,弦所在直线方程为
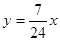 或
或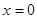 …………12分
…………12分因为直线过原点可设直线方程为y=kx,再利用圆心到直线的距离d,弦长,半径三者之间的关系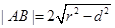 ,建立关于k的方程,求出k值.
,建立关于k的方程,求出k值.
x2+y2-6x-8y=0即(x-3)2+(y-4)2=25,
若直线有斜率,则设所求直线为y=kx.…………2分
∵圆半径为5,
∴圆心M(3,4)到该直线距离为3,…………4分
∴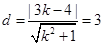 ,…………6分
,…………6分
∴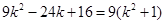 ,∴
,∴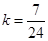 . …………8分
. …………8分
∴所求直线为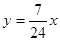 …………9分
…………9分
若直线没有斜率,即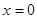 ,直线与圆两交点分别是A(0,0)、B(0,8),
,直线与圆两交点分别是A(0,0)、B(0,8),
弦长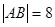 ,…………11分
,…………11分
综上,弦所在直线方程为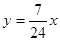 或
或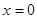 …………12分
…………12分
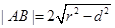 ,建立关于k的方程,求出k值.
,建立关于k的方程,求出k值.x2+y2-6x-8y=0即(x-3)2+(y-4)2=25,
若直线有斜率,则设所求直线为y=kx.…………2分
∵圆半径为5,
∴圆心M(3,4)到该直线距离为3,…………4分
∴
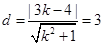 ,…………6分
,…………6分 ∴
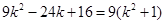 ,∴
,∴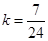 . …………8分
. …………8分 ∴所求直线为
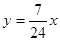 …………9分
…………9分 若直线没有斜率,即
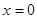 ,直线与圆两交点分别是A(0,0)、B(0,8),
,直线与圆两交点分别是A(0,0)、B(0,8),弦长
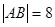 ,…………11分
,…………11分 综上,弦所在直线方程为
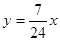 或
或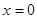 …………12分
…………12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
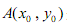 是曲线C上的一个定点,过点A任意作两条倾斜角互补的直线,分别与曲线C相交于另外两点P 、Q.
是曲线C上的一个定点,过点A任意作两条倾斜角互补的直线,分别与曲线C相交于另外两点P 、Q.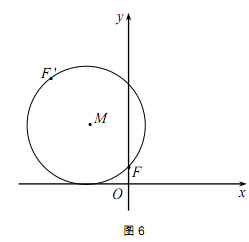
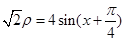 与曲线
与曲线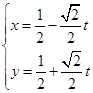 的位置关系是( )。
的位置关系是( )。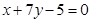 截圆
截圆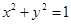 所得的两段弧长之差的绝对值是
所得的两段弧长之差的绝对值是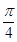

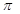
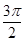
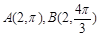 ,C是曲线
,C是曲线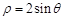 上任意一点,则
上任意一点,则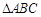 的面积的最小值等于 .
的面积的最小值等于 .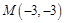 的直线
的直线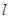 与圆
与圆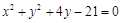 相交于
相交于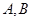 两点,若弦
两点,若弦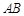 的长为
的长为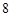 ,求直线
,求直线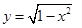 与直线
与直线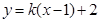 有两个交点时,实数
有两个交点时,实数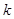 的取值范围是( )
的取值范围是( )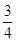 ≤k<1
≤k<1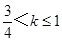
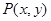 是圆
是圆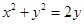 上的动点, (13分)
上的动点, (13分)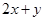 的取值范围
的取值范围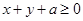 恒成立,求实数
恒成立,求实数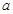 的取值。
的取值。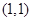 在圆
在圆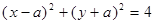 的内部,则
的内部,则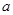 的取值范围是
的取值范围是