题目内容
已知函数y=f(x)的定义域为R+,对任意x,y∈R+,有恒等式f(xy)=f(x)+f(y);且当x>1时,f(x)<0.
(1)求f(1)的值;
(2)求证:当x∈R+时,恒有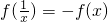 ;
;
(3)求证:f(x)在(0,+∞)上为减函数;
(4)由上一小题知:f(x)是(0,+∞)上的减函数,因而f(x)的反函数f-1(x)存在,试根据已知恒等式猜想f-1(x)具有的性质,并给出证明.
解:(1)令x=y=1,则f(1)=2f(1),∴f(1)=0
(2)证明:令y= ,则f(1)=f(x)+f(
,则f(1)=f(x)+f( ),∴
),∴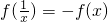
(3)证明:设任意x,y∈R+,且x<y, =a>1
=a>1
则f(x)-f(y)=f(x)-f(x•a)=f(x)-f(x)-f(a)=-f(a)
∵当x>1时,f(x)<0
∴f(a)<0,-f(a)>0
∴f(x)>f(y)
∴f(x)在(0,+∞)上为减函数
(4)猜想f-1(x)具有的性质,f-1(0)=1
证明:因为原函数与反函数关于直线y=x对称,
∵f(1)=0
∴f-1(0)=1
分析:(1)令x=y=1,代入恒等式f(xy)=f(x)+f(y)即可
(2)令y= ,则f(1)=f(x)+f(
,则f(1)=f(x)+f( ),由(1)即可得结论
),由(1)即可得结论
(3)设任意x,y∈R+,且x<y,利用函数单调性定义和已知当x>1时,f(x)<0,即可证明f(x)在(0,+∞)上为减函数
(4)利用互为反函数的函数图象的对称性,即可得反函数的性质
点评:本题考查了函数抽象表达式的应用,解题时要认真观察,熟练运用单调性定义及函数图象的对称性解题
(2)证明:令y=
 ,则f(1)=f(x)+f(
,则f(1)=f(x)+f( ),∴
),∴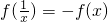
(3)证明:设任意x,y∈R+,且x<y,
 =a>1
=a>1则f(x)-f(y)=f(x)-f(x•a)=f(x)-f(x)-f(a)=-f(a)
∵当x>1时,f(x)<0
∴f(a)<0,-f(a)>0
∴f(x)>f(y)
∴f(x)在(0,+∞)上为减函数
(4)猜想f-1(x)具有的性质,f-1(0)=1
证明:因为原函数与反函数关于直线y=x对称,
∵f(1)=0
∴f-1(0)=1
分析:(1)令x=y=1,代入恒等式f(xy)=f(x)+f(y)即可
(2)令y=
 ,则f(1)=f(x)+f(
,则f(1)=f(x)+f( ),由(1)即可得结论
),由(1)即可得结论(3)设任意x,y∈R+,且x<y,利用函数单调性定义和已知当x>1时,f(x)<0,即可证明f(x)在(0,+∞)上为减函数
(4)利用互为反函数的函数图象的对称性,即可得反函数的性质
点评:本题考查了函数抽象表达式的应用,解题时要认真观察,熟练运用单调性定义及函数图象的对称性解题

练习册系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足