Question

【题目】已知三棱锥P﹣ABC的所有棱长为1．M是底面△ABC内部一个动点（包括边界），且M到三个侧面PAB，PBC，PAC的距离h1，h2，h3成单调递增的等差数列，记PM与AB，BC，AC所成的角分别为α，β，γ，则下列正确的是（　　）

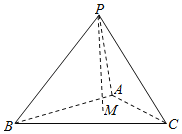
A.α＝βB.β＝γC.α＜βD.β＜γ

Answer 1

【答案】D

【解析】

PM与AB，BC，AC所成的角分别为α，β，γ，即比较OM与AB，BC，AC夹角的大小，然后在△ABC中解决问题, 由于d1＜d2＜d3，可知M在如图阴影区域（不包括边界）

从图中可以看出，OM与BC所成角小于OM与AC所成角,即得解.

依题意知正四面体P﹣ABC的顶点P在底面ABC的射影是正三角形ABC的中心O，

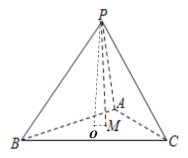
由余弦定理可知，

cosα＝cos∠PMOcos＜MO，AB＞，其中＜MO，AB＞表示直线MO与AB的夹角，

同理可以将β，γ转化，

cosβ＝cos∠PMOcos＜MO，BC＞，其中＜MO，BC＞表示直线MO与BC的夹角，

cosγ＝cos∠PMOcos＜MO，AC＞，其中＜MO，AC＞表示直线MO与AC的夹角，

由于∠PMO是公共的，因此题意即比较OM与AB，BC，AC夹角的大小，

设M到AB，BC，AC的距离为d1，d2，d3 则d1＝sin，其中θ是正四面体相邻两个面所成角，sinθ，

所以d1，d2，d3成单调递增的等差数列，然后在△ABC中解决问题

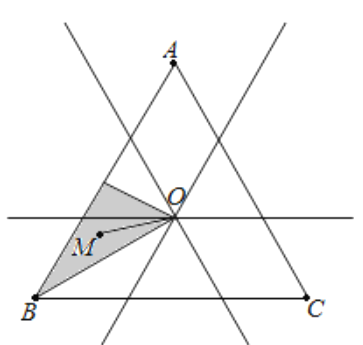
由于d1＜d2＜d3，可知M在如图阴影区域（不包括边界）

从图中可以看出，OM与BC所成角小于OM与AC所成角，所以β＜γ，

故选：D．