设集合A={(x.y)|x2+y2=1}.B={(x.y)|y=2x}.则A∩B子集的个数是( )A．2B．3C．8D．4 题目和参考答案——青夏教育精英家教网——

题目内容

2．设集合A={（x，y）|x²+y²=1}，B={（x，y）|y=2^x}，则A∩B子集的个数是（　　）

A．

2

B．

3

C．

8

D．

4

分析画出两函数的图象，找出交点个数，即可确定出两交集个数即可．

解答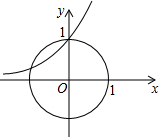解：集合A中x²+y²=1，表示原点为圆心，1为半径的圆，集合B中y=2^x，表示指数函数，
在同一个坐标系中画出图象，得到两函数有两个交点，
则A∩B子集的个数是2²=4．
故选：D．

点评此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．

练习册系列答案

期末测试卷系列答案

小学培优总复习系列答案

小学科学探究手册系列答案

小学达标训练系列答案

小学毕业综合复习系列答案

小学毕业特训卷系列答案

小学毕业升学总复习系列答案

小学毕业升学模拟试卷系列答案

打好双基名校名师模拟卷系列答案

归类复习模拟试卷系列答案

相关题目

12．已知矩阵A的逆矩阵A^-1=$[\begin{array}{l}{\frac{\sqrt{2}}{2}}&{\frac{\sqrt{2}}{2}}\\{-\frac{\sqrt{2}}{2}}&{\frac{\sqrt{2}}{2}}\end{array}]$．求曲线xy=1在矩阵A所对应的变换作用下所得的曲线方程．

13．在四棱柱ABCD-A₁B₁C₁D₁中，侧棱DD₁⊥底面ABCD，P为底面ABCD内的一个动点，当△D₁PC的面积为定值b（b＞0）时，点P在底面ABCD上的运动轨迹为（　　）

10．已知曲线C的方程为$\frac{x^2}{4}+\frac{y^2}{5}$=1，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为$ρcos（θ-\frac{π}{4}）=2\sqrt{2}$．
（Ⅰ）求直线l的直角坐标方程；
（Ⅱ）已知M是曲线C上任意一点，求点M到直线l距离的最小值．

已知a，b，c是△ABC对边，且a+b=$\sqrt{3}$csinA+ccosA，为BC的中点，且AD=2，求△ABC最大值．

7．设不等式组$\left\{\begin{array}{l}{3x+y-10≥0}\\{x-y-6≤0}\\{x+3y-6≤0}\end{array}\right.$表示的平面区域为D，若函数y=log_ax（a＞0且a≠1）的图象上存在区域D上的点，则实数a的取值范围是（　　）

（0，$\frac{1}{2}$]∪[3，+∞）

[$\frac{1}{2}$，1）∪[3，+∞）

（0，$\frac{1}{2}$∪（1，3]

[$\frac{1}{2}$，1）∪（1，3]

已知四边形ABCD是边长为$\sqrt{3}$的菱形，对角线AC=2$\sqrt{2}$．分别过点B，C，D向平面ABCD外作3条相互平行的直线BE、CF、DG，其中点E，F在平面ABCD同侧，CF=8，且平面AEF与直线DG相交于点G，GE∩AF=P，AC∩BD=O，连结OP．
（Ⅰ）证明：OP∥DG；
（Ⅱ）当点F在平面ABCD内的投影恰为O点时，求四面体FACE的体积．

如图，在四棱锥A-BCED中，△ABC为正三角形，EC⊥平面ABC，BD⊥平面ABC，M为棱EA的中点，CE=2BD．
（Ⅰ）求证：DM∥平面ABC；
（Ⅱ）求证：平面BDM⊥平面ECA．

5．已知函数f（x）=me^x-$\frac{lnx}{x}$-ne^xx³，且函数f（x）在点（1，e）处的切线与直线x-（2e+1）y-3=0垂直，求证：当x∈（0，1）时，f（x）＞0．