题目内容
7.设不等式组$\left\{\begin{array}{l}{3x+y-10≥0}\\{x-y-6≤0}\\{x+3y-6≤0}\end{array}\right.$表示的平面区域为D,若函数y=logax(a>0且a≠1)的图象上存在区域D上的点,则实数a的取值范围是( )| A. | (0,$\frac{1}{2}$]∪[3,+∞) | B. | [$\frac{1}{2}$,1)∪[3,+∞) | C. | (0,$\frac{1}{2}$∪(1,3] | D. | [$\frac{1}{2}$,1)∪(1,3] |
分析 结合二元一次不等式(组)与平面区域的关系画出其表示的平面区域,再利用函数y=logax(a>0且a≠1)的图象特征,结合区域的角上的点即可解决问题.
解答  解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
若0<a<1,则由图象可知点B在对数函数的图象或图象的下面,
由$\left\{\begin{array}{l}{3x+y-10=0}\\{x-y-6=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=4}\\{y=-2}\end{array}\right.$,即B(4,-2),
此时满足loga4≥-2,
解得0<a≤$\frac{1}{2}$.
若a>1,当A在对数函数的图象或图象的上方时,满足条件,
由$\left\{\begin{array}{l}{3x+y-10=0}\\{x+3y-6=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$,即A(3,1),
此时满足loga3≤1,解得a≥3,
综上0<a≤$\frac{1}{2}$或a≥3.
∴实数a的取值范围是(0,$\frac{1}{2}$]∪[3,+∞),
故选:A.
点评 本题主要考查线性规划的应用,利用对数函数的图象和性质,通过数形结合是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.若a∈R,则“a=1”是“直线x+y+a=0与圆x2+y2=1相交”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19.命题p:“存在x0∈[1,+∞),使得(log23)x0≥1”,则命题p的否定是( )
| A. | 存在x0∈[1,+∞),使得(log23)x0<1 | B. | 存在x0∈[1,+∞),使得(log23)x0≥1 | ||
| C. | 任意x∈[1,+∞),都有(log23)x<1 | D. | 任意x∈[1,+∞),都有(log23)x≥1 |
16.已知直线$\left\{\begin{array}{l}x=2+t\\ y=1+t\end{array}\right.$(t为参数)与曲线M:ρ=2cosθ交于P,Q两点,则|PQ|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
10.设函数f(x)=$\frac{{a}^{2}+asinx+2}{{a}^{2}+acosx+2}$(x∈R)的最大值为M(a),最小值为m(a),则( )
| A. | ?a∈R,M(a)•m(a)=1 | B. | ?a∈R,M(a)+m(a)=2 | C. | ?a0∈R,M(a0)+m(a0)=1 | D. | ?a0∈R,M(a0)•m(a0)=2 |
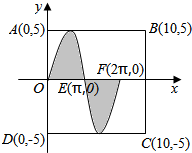 国家AAAAA级八里河风景区五一期间举办“管仲杯”投掷飞镖比赛.每3人组成一队,每人投掷一次.假设飞镖每次都能投中靶面,且靶面上每点被投中的可能性相同.某人投中靶面内阴影区域记为“成功”(靶面正方形ABCD如图所示,其中阴影区域的边界曲线近似为函数y=Asinx的图象).每队有3人“成功”获一等奖,2人“成功”获二等奖,1人“成功”获三等奖,其他情况为鼓励奖(即四等奖)(其中任何两位队员“成功”与否互不影响).
国家AAAAA级八里河风景区五一期间举办“管仲杯”投掷飞镖比赛.每3人组成一队,每人投掷一次.假设飞镖每次都能投中靶面,且靶面上每点被投中的可能性相同.某人投中靶面内阴影区域记为“成功”(靶面正方形ABCD如图所示,其中阴影区域的边界曲线近似为函数y=Asinx的图象).每队有3人“成功”获一等奖,2人“成功”获二等奖,1人“成功”获三等奖,其他情况为鼓励奖(即四等奖)(其中任何两位队员“成功”与否互不影响).