题目内容
【题目】已知椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,直线l1经过椭圆的上顶点A和右顶点B,并且和圆x2+y2=
,直线l1经过椭圆的上顶点A和右顶点B,并且和圆x2+y2=![]() 相切.
相切.
(1)求椭圆C的方程;
(2)设直线![]()
![]() 与椭圆C相交于M、N两点,以线段OM、ON为邻边作平行四边形OMPN,其中顶点P在椭圆C上,O为坐标原点,求|OP|的取值范围.
与椭圆C相交于M、N两点,以线段OM、ON为邻边作平行四边形OMPN,其中顶点P在椭圆C上,O为坐标原点,求|OP|的取值范围.
【答案】(1)![]() +y2=1
+y2=1
(2)[1,![]() ]
]
【解析】
(1)直线![]() 的方程为
的方程为![]() ;由直线l1与圆
;由直线l1与圆![]() 相切与
相切与![]() ,即可解出
,即可解出![]() ,即可得出答案.
,即可得出答案.
(2)联立直线与椭圆,设![]() ,根据韦达定理得到点
,根据韦达定理得到点![]()
![]() ,
,![]() ,将其代入椭圆可得到:
,将其代入椭圆可得到:![]() ,代入
,代入![]() ,化简消
,化简消![]() 后再由
后再由![]() ,即可得出|OP|的取值范围.
,即可得出|OP|的取值范围.
(1)由已知可得![]() =
=![]() =
=![]() ,所以
,所以![]() ,即
,即![]() .
.
又椭圆的上顶点![]() ,右顶点
,右顶点![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,即x+2y-a=0.
,即x+2y-a=0.
因为直线![]() 与圆
与圆![]() 相切,所以圆心
相切,所以圆心![]() 到直线
到直线![]() 的距离等于圆的半径,即
的距离等于圆的半径,即![]() =
=![]() ,解得a=2.
,解得a=2.
所以b=1,故椭圆C的方程为![]() .
.
(2)将直线l2的方程和椭圆C的方程联立得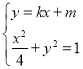
消去y,化简整理得![]() .
.
故![]() ,即
,即![]() .
.
设![]() ,
,
则由根与系数之间的关系可得![]()
![]() .
.
因为四边形OMPN为平行四边形,所以![]() =
=![]() .故点P(
.故点P(![]() ,
,![]() ).
).
由点P在椭圆上可得 +(
+(![]() )2=1,
)2=1,
整理得![]() .
.
因为![]() ,所以
,所以![]() ,即
,即![]()
![]() .
.![]()
则![]() (
(![]() )2+(
)2+(![]() )2
)2
=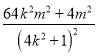 =
=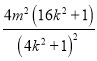 =
=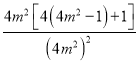
=![]() =4-
=4-![]() .
.
因为![]() ,所以m2∈[
,所以m2∈[![]() ,1],所以4-
,1],所以4-![]() ∈[1,
∈[1,![]() ],故|OP|∈[1,
],故|OP|∈[1,![]() ].
].

练习册系列答案
相关题目