题目内容
已知f(x)=
,若f(x)≤k(x-1)恒成立,则k的取值范围是( )
|
| A、(1,+∞) |
| B、(-∞,0] |
| C、(0,1) |
| D、[0,1] |
考点:分段函数的应用
专题:函数的性质及应用
分析:先作出函数f(x)的图象,将直线y=k(x-1)从x轴开始按逆时钟方向绕点(1,0)旋转,至与函数y=lnx(x>0)的图象相切时,能保证f(x)≤k(x-1)成立,从而获得k的取值范围.
解答:解:由f(x)的解析式画出其图象,如右图所示,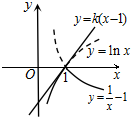
设曲线y=lnx(x>0)在点(1,0)处的切线的斜率为k0,
由直线y=k(x-1)的位置变化知,若f(x)≤k(x-1)恒成立,则0≤k≤k0,
又由y′=(lnx)′=
,得k0=1,
所以0≤k≤1.
故选D.
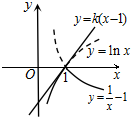
设曲线y=lnx(x>0)在点(1,0)处的切线的斜率为k0,
由直线y=k(x-1)的位置变化知,若f(x)≤k(x-1)恒成立,则0≤k≤k0,
又由y′=(lnx)′=
| 1 |
| x |
所以0≤k≤1.
故选D.
点评:1.本题考查了分段函数的应用,利用图象关系进行处理,体现了数形结合思想的运用.
2.对于分段函数问题,关键是掌握分界点处的情况.
2.对于分段函数问题,关键是掌握分界点处的情况.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
e,π分别是自然对数的底数和圆周率,则下列不等式中不成立的是( )
A、
| |||||
B、logπ
| |||||
| C、logπe+(logeπ)2>2 | |||||
| D、ee-e>eπ-π |
已知函数f(x)满足:①定义域为R;②对任意x∈R,有f(x+2)=2f(x);③当x∈[-1,1]时,f(x)=
.若函数g(x)=
,则函数y=f(x)-g(x)在区间[-5,5]上零点的个数是( )
| 1-x2 |
|
| A、7 | B、8 | C、9 | D、10 |
已知函数f(x)=
,且g(x)=f(x)-mx-m在(-1,1]内有且仅有两个不同的零点,则实数m的取值范围是( )
|
A、(-
| ||||
B、(-
| ||||
C、(-
| ||||
D、(-
|
已知函数f(x)=
若函数y=g(x)的图象与函数y=f-1(x-1)的图象关于直线y=x对称,则g(11)的值是( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
已知f(x)=
,则f(2014)=( )
|
| A、-1 | B、2 | C、0 | D、1 |
下列说法错误的是( )
| A、平面α与平面β相交,它们只有有限个公共点 | B、经过一条直线和这条直线外的一点,有且只有一个平面 | C、经过两条相交直线,有且只有一个平面 | D、如果两个平面有三个不共线的公共点,那么这两个平面重合 |