题目内容
20.已知三点P1(1,1,0).P2(0,1,1)和P3(1,0,1),O为坐标原点,则|$\overrightarrow{O{P}_{1}}+\overrightarrow{O{P}_{2}}+\overrightarrow{O{P}_{3}}$|=$\sqrt{3}$.分析 根据空间向量的坐标表示与运算,求出$\overrightarrow{{OP}_{1}}$+$\overrightarrow{{OP}_{2}}$+$\overrightarrow{{OP}_{3}}$的坐标表示,再求模长即可.
解答 解:∵点P1(1,1,0),P2(0,1,1)和P3(1,0,1),
∴$\overrightarrow{{OP}_{1}}$=(1,1,0),
$\overrightarrow{{OP}_{2}}$=(0,1,1),
$\overrightarrow{{OP}_{3}}$=(1,0,1),
∴|$\overrightarrow{{OP}_{1}}$+$\overrightarrow{{OP}_{2}}$+$\overrightarrow{{OP}_{3}}$|=(2,2,2),
∴|$\overrightarrow{O{P}_{1}}+\overrightarrow{O{P}_{2}}+\overrightarrow{O{P}_{3}}$|=$\sqrt{{2}^{2}{+2}^{2}{+2}^{2}}$=2$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查了空间向量的坐标表示与计算问题,是基础题目.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
8.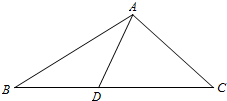 如图,在△ABC上,D是BC上的点,且AC=CD,2AC=$\sqrt{3}$AD,AB=2AD,则sinB等于( )
如图,在△ABC上,D是BC上的点,且AC=CD,2AC=$\sqrt{3}$AD,AB=2AD,则sinB等于( )
 如图,在△ABC上,D是BC上的点,且AC=CD,2AC=$\sqrt{3}$AD,AB=2AD,则sinB等于( )
如图,在△ABC上,D是BC上的点,且AC=CD,2AC=$\sqrt{3}$AD,AB=2AD,则sinB等于( )| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{6}$ | D. | $\frac{\sqrt{3}}{6}$ |
9.已知直线的倾斜角为45°,则该直线的斜率为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | 1 | D. | 0 |