题目内容
设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+b(b为常数),则f(﹣1)=( )
| A.﹣3 | B.﹣1 | C.1 | D.3 |
A
因为f(x)为定义在R上的奇函数,
所以f(0)=20+2×0+b=0,
解得b=﹣1,
所以当x≥0时,f(x)=2x+2x﹣1,
又因为f(x)为定义在R上的奇函数,
所以f(﹣1)=﹣f(1)=﹣(21+2×1﹣1)=﹣3,
故选A.
所以f(0)=20+2×0+b=0,
解得b=﹣1,
所以当x≥0时,f(x)=2x+2x﹣1,
又因为f(x)为定义在R上的奇函数,
所以f(﹣1)=﹣f(1)=﹣(21+2×1﹣1)=﹣3,
故选A.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
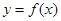 的图象与函数
的图象与函数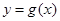 的图象关于直线
的图象关于直线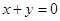 对称,则
对称,则
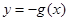
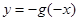
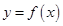 为偶函数,当
为偶函数,当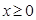 时,
时,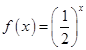 ,则不等式
,则不等式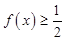 的解集为______.
的解集为______.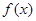 满足
满足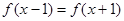 ,且在
,且在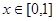 时,
时,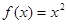 ,则关于
,则关于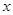 的方程
的方程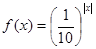 在
在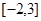 上的根的个数是
上的根的个数是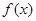 是定义在R上的奇函数.当x<0时,
是定义在R上的奇函数.当x<0时,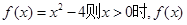 的解析式为 ;不等式f(x)<0的解集为 .
的解析式为 ;不等式f(x)<0的解集为 .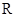 上的偶函数
上的偶函数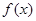 满足
满足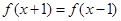 ,且当
,且当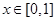 时,
时,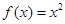 ,则关于
,则关于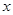 的方程
的方程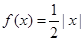 在
在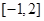 上根的个数是( )
上根的个数是( )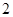
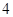

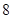
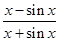
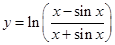 的图象大致是( )
的图象大致是( )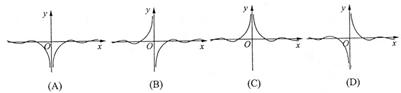
 则f(2014)=________.
则f(2014)=________.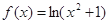 的图象大致是( )
的图象大致是( )