题目内容
8.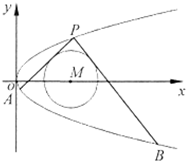 已知曲线C:y2=2px(p>0)过定点(1,1),点P是曲线C上的动点,过点P的圆M:(x-t)2+y2=1(t>1)的切线l1,l2分别交曲线C于另外两点A,B.
已知曲线C:y2=2px(p>0)过定点(1,1),点P是曲线C上的动点,过点P的圆M:(x-t)2+y2=1(t>1)的切线l1,l2分别交曲线C于另外两点A,B.(Ⅰ)求曲线C的方程;
(Ⅱ)若t=$\sqrt{2}$,点P为原点,判断直线AB与圆的位置关系;
(Ⅲ)对任意的动点P,是否存在实数t,使得直线AB与圆相切?若存在,求出t的值;若不存在,请说明理由.
分析 (Ⅰ)将点(1,1)代入,即可求得p,进而得到抛物线方程;
(Ⅱ)若t=$\sqrt{2}$,点P为原点,设切线方程为y=kx,由直线和圆相切的条件,可得k,再代入抛物线方程,求得A,B的坐标,求得AB的方程,由直线和圆位置关系的判断,即可得到;
(Ⅲ)取P(0,0),圆(x-t)2+y2=1(t>1),切线为y=kx,运用点到直线的距离公式,求得k,再将直线方程代入抛物线方程,解得A,B,由AB的方程,运用点到直线的距离,结合相切的条件可得t=2,再对t=2,任意的P,直线AB和圆相切,证明即可.
解答 解:(Ⅰ)曲线C:y2=2px(p>0)过定点(1,1),
即有1=2p,解得p=$\frac{1}{2}$,
则曲线C的方程为y2=x;
(Ⅱ)若t=$\sqrt{2}$,点P为原点,则圆为(x-$\sqrt{2}$)2+y2=1,
设切线方程为y=kx,
由$\frac{|\sqrt{2}k|}{\sqrt{1+{k}^{2}}}$=1,解得k=±1,
即有切线方程为y=±x,
代入抛物线方程可得A(1,1),B(1,-1),
由圆心($\sqrt{2}$,0)到直线x=1的距离为$\sqrt{2}$-1<1,
即有直线AB和圆相交;
(Ⅲ)取P(0,0),圆(x-t)2+y2=1(t>1),切线为y=kx,
由$\frac{|kt|}{\sqrt{1+{k}^{2}}}$=1,解得k2=$\frac{1}{{t}^{2}-1}$,①
将直线y=±kx代入抛物线方程y2=x,
解得A($\frac{1}{{k}^{2}}$,$\frac{1}{k}$),B($\frac{1}{{k}^{2}}$,-$\frac{1}{k}$),
直线AB的方程为x=$\frac{1}{{k}^{2}}$,
若直线和圆相切,可得$\frac{1}{{k}^{2}}$=1+t②
由①②解得t=2或-1(舍去).
综上可得,对任意的动点P,直线AB与圆相切,必有t=2.
下证t=2时,对任意的动点P,直线AB和圆相切.
理由如下:设P(a2,a),l:x=m(y-a)+a2,A(y12,y1),B(y22,y2),
由$\frac{|2+ma-{a}^{2}|}{\sqrt{1+{m}^{2}}}$=1,可得(a2-1)m2-2(a2-2)am+(a2-2)2-1=0,
m1+m2=$\frac{2({a}^{2}-2)a}{{a}^{2}-1}$,m1m2=$\frac{({a}^{2}-2)^{2}-1}{{a}^{2}-1}$,
又直线与曲线相交于A,B,
由x=m(y-a)+a2,代入抛物线方程y2-my+ma-a2=0,
y12=m1(y1-a)+a2,y22=m2(y2-a)+a2,
则a,y1是方程y2=m1(y-a)+a2的两根,
即有ay1=am1-a2,即为y1=m1-a,同理y2=m2-a.
则有A((m1-a)2,m1-a),B((m2-a)2,m2-a),
直线AB:y-(m1-a)=$\frac{1}{{m}_{1}+{m}_{2}-2a}$(x-(m1-a)2),
即为y-(m1-a)=$\frac{2a}{1-{a}^{2}}$(x-(m1-a)2),
则圆心(2,0)到直线AB的距离为d=$\frac{|\frac{4a}{1-{a}^{2}}+{m}_{1}-a-\frac{2a}{1-{a}^{2}}({m}_{1}-a)^{2}|}{\sqrt{1+(\frac{2a}{1-{a}^{2}})^{2}}}$,
由(a2-1)m12-2(a2-2)am1+(a2-2)2-1=0,
代入上式,化简可得d=$\frac{|{a}^{2}+1|}{{a}^{2}+1}$=1,
则有对任意的动点P,存在实数t=2,使得直线AB与圆相切.
点评 本题考查抛物线的方程和性质,主要考查抛物线的方程的运用,注意联立直线方程和抛物线方程,运用韦达定理,同时考查直线和圆的位置关系:相切的条件,具有一定的运算量,属于中档题.

| A. | x=-$\frac{1}{8}$ | B. | x=$\frac{1}{8}$ | C. | y=-$\frac{1}{8}$ | D. | y=$\frac{1}{8}$ |
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
| A. | 3 | B. | 2$\sqrt{2}$ | C. | $\sqrt{11}$ | D. | $\sqrt{10}$ |