题目内容
17.已知△ABC的内角∠A、∠B、∠C所对的边长分别为a、b、c且b=3,c=1,∠A=2∠B,求a的值.分析 利用正弦定理列出关系式,把b=3,∠A=2∠B代入得到关于a与cosB的关系式,再利用余弦定理列出关系式,把b,c,cosA=cos2B代入得到关于a与cosB的关系式,联立求出a的值即可.
解答 解:∵b=3,∠A=2∠B,
∴由正弦定理得:$\frac{a}{sinA}$=$\frac{b}{sinB}$,即$\frac{a}{sin2B}$=$\frac{3}{sinB}$,即a=6cosB,
由余弦定理得:a2=b2+c2-2bccosA=9+1-6cosA=10-6cos2B=10-6(2cos2B-1)=16-12cos2B,
把a=6cosB代入得:36cos2B=16-12cos2B,即cos2B=$\frac{1}{3}$,
∵∠A=2∠B,∴∠B为锐角,即cosB>0,
∴cosB=$\frac{\sqrt{3}}{3}$,
则a=6×$\frac{\sqrt{3}}{3}$=2$\sqrt{3}$.
点评 此题考查了正弦、余弦定理,以及二倍角的余弦函数公式,熟练掌握正弦、余弦定理是解本题的关键.

练习册系列答案
相关题目
7.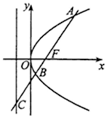 如图,过抛物线y2=2px(p>0)焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为( )
如图,过抛物线y2=2px(p>0)焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为( )
 如图,过抛物线y2=2px(p>0)焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为( )
如图,过抛物线y2=2px(p>0)焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为( )| A. | y2=3x | B. | y2=9x | C. | y2=$\frac{3}{2}$x | D. | y2=$\frac{9}{2}$x |
12.下列关于函数f(x)=$\sqrt{3}$cos2x+tan(x-$\frac{π}{4}$)的图象叙述正确的是( )
| A. | 关于原点对称 | B. | 关于y轴对称 | ||
| C. | 关于点($\frac{π}{4}$,0)对称 | D. | 关于直线x=$\frac{π}{4}$对称 |
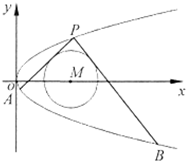 已知曲线C:y2=2px(p>0)过定点(1,1),点P是曲线C上的动点,过点P的圆M:(x-t)2+y2=1(t>1)的切线l1,l2分别交曲线C于另外两点A,B.
已知曲线C:y2=2px(p>0)过定点(1,1),点P是曲线C上的动点,过点P的圆M:(x-t)2+y2=1(t>1)的切线l1,l2分别交曲线C于另外两点A,B.