题目内容

函数f（k）=|k-1|+|k-2|+…+|k-15|，k∈N₊且1≤k≤15
（1）分别计算f （2）、f （5）的值；
（2）当k为何值时，f（k）取最小值？最小值为多少？

解：（1）∵函数f（k）=|k-1|+|k-2|+…+|k-15|，
∴f（2）=|2-1|+|2-2|+|2-3|+|2-4|+…+|2-15|=1+0+1+2+…+13=92；
f（5）=|5-1|+|5-2|+|5-3|+|5-4|+|5-5|+|5-6|+|5-7|+…+|5-15|=4+3+2+1+0+1+2+…+10=65；
（2）f（k）=（k-1）+（k-2）+…+1+0+1+2+…+（15-k）
= $\text{[math]}$
$\text{[math]}$
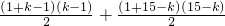
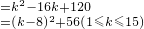
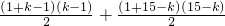
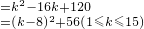
所以当k=8时，f（k）有最小值56
分析：（1）由已知中函数f（k）的解析式，将2和5代入函数解析式，即可求出f （2）、f （5）的值；
（2）由函数f（k）的解析式，利用零点分段法，我们可以求出f（k）的表达式（整式不含绝对值符号），进而根据二次函数的图象和性质求出答案．
点评：本题以绝对值函数为载体考查了二次函数的性质，零点分段法，等差数列的求和，代入法求函数值等知识点，难度中等．

练习册系列答案

畅响双优卷系列答案

初中满分冲刺卷系列答案

52045单元与期末系列答案

精彩考评单元测评卷系列答案

导学案快乐学习系列答案

孟建平各地期末试卷精选系列答案

名师三导学练考系列答案

轻松小卷系列答案

提分百分百检测卷系列答案

权威考卷系列答案

相关题目

设函数f(x)＝ax²＋bx＋1(a、b∈R)

(1)若f(－1)＝0，则对任意实数均有f(x)≥0成立，求f(x)的表达式．

(2)(文)在(1)的条件下，当x∈[－2，2]时，g(x)＝f(x)－kx是单调函数，求实数k的取值范围．

(理)在(1)的条件下，当x∈[－2，2]时，g(x)＝xf(x)－kx是单调递增，求实数k的取值范围．

函数f(x)的定义域为R，数列{a_n}满足a_n＝f(a_n－1)(n∈N^*且n≥2)．

(Ⅰ)若数列{a_n}是等差数列，a₁≠a₂，且f(a_n)－f(a_n－1)＝k(a_n－a_n－1)(k为非零常数，n∈N^*且n≥2)，求k的值；

(Ⅱ)若f(x)＝kx(k＞1)，a₁＝2，b_n＝lna_n(n∈N^*)，数列{b_n}的前n项和为S_n，对于给定的正整数m，如果的值与n无关，求k的值．

已知函数f（x）=sin（2x+φ），其中φ为常数，若f（x）≤|f（ $数学公式$ ）|对x∈R恒成立，且f（ $数学公式$ ）＞f（ $数学公式$ ），则函数f（x）的单调减区间是

A.
[kπ- $数学公式$ ，kπ+ $数学公式$ ]（k∈Z）
B.
[kπ- $数学公式$ ，kπ+ $数学公式$ ]（k∈Z）
C.
[kπ+ $数学公式$ ，kπ+ $数学公式$ ]（k∈Z）
D.
[kπ+ $数学公式$ ，kπ+ $数学公式$ ]（k∈Z）

设函数f（x）=asin2x+bcos2x，其中a，b∈R．ab≠0，若f（x）≤|f（ $数学公式$ ）|对一切x∈R恒成立，则
①f（ $数学公式$ ）=0；　②|f（ $数学公式$ ）|＜|f（ $数学公式$ ）|；
③函数y=f（x）既不是奇函数也不是偶函数；
④函数y=f（x）的单调递增区间是：[kπ+ $数学公式$ ，kπ+ $数学公式$ ]（k∈Z）；
⑤经过点（a，b）的所有直线均与函数y=f（x）的图象相交．
以上结论正确的是________（写出所有正确结论的编号）．

已知函数f(k)=|k-1|+|k-2|+…+|k-25|，k∈N₊且1≤k≤25。
（1）分别计算f(2)、f(5)、f(12)的值；
（2）当k为何值时，f(k)取最小值？最小值为多少？