题目内容
设函数f(x)=ax2+bx+1(a、b∈R)
(1)若f(-1)=0,则对任意实数均有f(x)≥0成立,求f(x)的表达式.
(2)(文)在(1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围.
(理)在(1)的条件下,当x∈[-2,2]时,g(x)=xf(x)-kx是单调递增,求实数k的取值范围.
答案:
解析:
解析:
|
解(1)∵f(-1)=0 又∵对任意实数均有f(x)≥0成立 (文)(2)解:g(x)=f(x)-kx ∵g(x)是单调函数 (理)(2)解:g(x)=xf(x)-kx=x(x2+2x+1)-kx=x3+2x2+(1-k)x |

练习册系列答案
相关题目
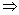 a-b+1=0
a-b+1=0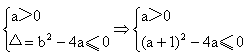
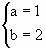 ∴f(x)=x2+2x+1
∴f(x)=x2+2x+1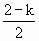 ≤-2或-
≤-2或-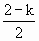 ≥2
≥2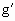 (x)=3x2+4x+1-k≥0在[-2,2]上恒成立
(x)=3x2+4x+1-k≥0在[-2,2]上恒成立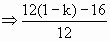 ≥0
≥0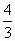
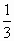
 ,x∈[0,+∞)
,x∈[0,+∞) (k∈R+).
(k∈R+).