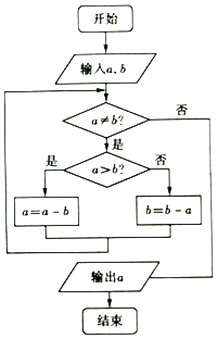
题目内容
【题目】已知圆O：x2+y2=1过椭圆C： 
（a＞b＞0）的短轴端点，P，Q分别是圆O与椭圆C上任意两点，且线段PQ长度的最大值为3． （Ⅰ）求椭圆C的方程；
（Ⅱ）过点（0，t）作圆O的一条切线交椭圆C于M，N两点，求△OMN的面积的最大值．
【答案】解：（Ⅰ）∵圆O过椭圆C的短轴端点，∴b=1， 又∵线段PQ长度的最大值为3，
∴a+1=3，即a=2，
∴椭圆C的标准方程为 
．
（Ⅱ）由题意可设切线MN的方程为y=kx+t，即kx﹣y+t=0，则 
，得k2=t2﹣1．①
联立得方程组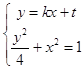 
，消去y整理得（k2+4）x2+2ktx+t2﹣4=0．
其中△=（2kt）2﹣4（k2+4）（t2﹣4）=﹣16t2+16k2+64=48＞0，
设M（x1 ， y1），N（x2 ， y2），则 
， 
，
则 
．②
将①代入②得 
，∴ 
，
而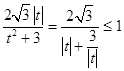 
，等号成立当且仅当 
，即 
．
综上可知：（S△OMN）max=1
【解析】（Ⅰ）由圆O过椭圆C的短轴端点b=1，线段PQ长度的最大值为3，a+1=3，a=2，即可求得椭圆方程；（Ⅱ）设直线MN的方程，由点到直线的距离公式，求得k2=t2﹣1，代入椭圆方程，由韦达定理及弦长公式求得丨MN丨，利用三角形的面积公式及基本不等式的性质，即可求得△OMN的面积的最大值．
阅读快车系列答案【题目】某重点中学为了解高一年级学生身体发育情况，对全校700名高一年级学生按性别进行分层抽样检查，测得身高（单位：cm）频数分布表如表1、表2． 表1：男生身高频数分布表
身高（cm） | [160，165） | [165，170） | [170，175） | [175，180） | [180，185） | [185，190） |
频数 | 2 | 5 | 14 | 13 | 4 | 2 |
表2：女生身高频数分布表
身高（cm） | [150，155） | [155，160） | [160，165） | [165，170） | [170，175） | [175，180） |
频数 | 1 | 7 | 12 | 6 | 3 | 1 |
（1）求该校高一女生的人数；
（2）估计该校学生身高在[165，180）的概率；
（3）以样本频率为概率，现从高一年级的男生和女生中分别选出1人，设X表示身高在[165，180）学生的人数，求X的分布列及数学期望．
