题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求证:对
时,求证:对![]() 时,
时, ![]() ;
;
(2)当![]() 时,讨论函数
时,讨论函数![]() 零点的个数.
零点的个数.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)函数求导![]() ,再求导得
,再求导得![]() 恒成立,又因为
恒成立,又因为![]() 恒成立;
恒成立;
(2)由(1)可知,当x≤0时,f″(x)≤0,可得 对x∈R,f′(x)≥0,即ex≥x+1,分类讨论当x≥-1时,当x<-1时,函数y=f(x)的零点个数即可得解;
当x<-1时,再分0≤m≤1和m<0两种情况进行讨论,由函数零点定理进行判断即可得到答案.
试题解析:,所以
(1)当![]() 时,
时, ![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,当
,当![]() 时,
时, ![]() ,即
,即![]() ,所以函数
,所以函数![]() 在
在![]() 上为增函数,即当
上为增函数,即当![]() 时,
时, ![]() ,所以当
,所以当![]() 时,
时, ![]() 恒成立,所以函数
恒成立,所以函数![]() 在
在![]() 上为增函数,又因为
上为增函数,又因为![]() ,所以当
,所以当![]() 时,对
时,对![]() 恒成立.
恒成立.
(2)由(1)知,当![]() 时,
时, ![]() ,所以
,所以![]() ,所以函数
,所以函数![]() 的减区间为
的减区间为![]() ,增函数为
,增函数为![]() .所以
.所以![]() ,所以对
,所以对![]()
![]() ,
, ![]() ,即
,即![]() .
.
①当![]() 时,
时, ![]() ,又
,又![]() ,
, ![]() ,即
,即![]() ,所以当
,所以当![]() 时,函数
时,函数![]() 为增函数,又
为增函数,又![]() ,所以当
,所以当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上有且仅有一个零点,且为
上有且仅有一个零点,且为![]() .
.
②当![]() 时,(ⅰ)当
时,(ⅰ)当![]() 时,
时, ![]() ,所以
,所以![]() ,所以函数
,所以函数![]() 在
在![]() 上递增,所以
上递增,所以![]() ,且
,且![]() ,故
,故![]() 时,函数
时,函数![]() 在区间
在区间![]() 上无零点.
上无零点.
(ⅱ)当![]() 时,
时, ![]() ,令
,令![]() ,则
,则![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增,
上单调递增, ![]() ,当
,当![]() 时,
时, 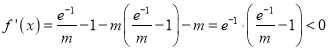 ,又曲线
,又曲线![]() 在区间
在区间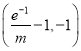 上不间断,所以
上不间断,所以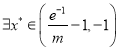 ,使
,使![]() ,故当
,故当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,所以函数
,所以函数![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]() ,又
,又![]() ,所以对
,所以对![]() ,又当
,又当![]() 时,
时, ![]() ,又
,又![]() ,曲线
,曲线![]() 在区间
在区间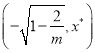 上不间断.所以
上不间断.所以![]() ,且唯一实数
,且唯一实数![]() ,使得
,使得![]() ,综上,当
,综上,当![]() 时,函数
时,函数![]() 有且仅有一个零点;当
有且仅有一个零点;当![]() 时,函数
时,函数![]() 有个两零点.
有个两零点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

