题目内容
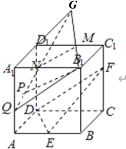
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E是AB的中点,F在CC1上,且CF=2FC1,点P是侧面AA1D1D(包括边界)上一动点,且PB1∥平面DEF,则tan∠ABP的取值范围为_____.

【答案】[![]() ].
].
【解析】
作出平面MNQB1∥平面DEF,推导出P的轨迹是线段QN,P在Q处,tan∠ABP取最小值,P在N处,tan∠ABP取最大值,由此能求出tan∠ABP的取值范围.
解:如下图所示,![]() 上取一点
上取一点![]() ,使得
,使得![]() ,
,
在![]() 上取中点
上取中点![]() ,连
,连![]() ,与
,与![]() 交于
交于![]() ,
,
则![]() ,所以
,所以![]() ,
,
即![]() 为
为![]() 中点,连
中点,连![]() 交
交![]() 于
于![]() ,因为
,因为![]() ,
,
所以![]() 为
为![]() 中位线,
中位线,![]()
在正方体![]() 中,
中,![]() 为
为![]() 中点,
中点,
则![]() 面
面![]() 面
面![]() ,
,
![]() 面
面![]() ,
,![]() ,同理可证
,同理可证![]() 面
面![]() ,
,
又![]() ,
,![]() 平面MNQB1
平面MNQB1![]() 平面DEF,
平面DEF,
∵PB1∥平面DEF,∴P的轨迹是线段QN,
设正方体![]() 棱长为
棱长为![]() ,
,
P在Q处,tan∠ABP取最小值tan![]() ,
,
P在N处,tan∠ABP取最大值tan∠ABP![]() .
.
∴tan∠ABP的取值范围为[![]() ].
].
故答案为:[![]() ].
].

 阅读快车系列答案
阅读快车系列答案【题目】随着电子产品的不断更新完善,更多的电子产品逐步走入大家的世界,给大家带来了丰富多彩的生活,但也带来了一些负面的影响,某公司随即抽取![]() 人对某电子产品是否对日常生活有益进行了问卷调查,并对参与调查的
人对某电子产品是否对日常生活有益进行了问卷调查,并对参与调查的![]() 人中的年龄层次以及意见进行了分类,得到的数据如下表所示:
人中的年龄层次以及意见进行了分类,得到的数据如下表所示:
|
| 总计 | |
认为某电子产品对生活有益 |
|
|
|
认为某电子产品对生活无益 |
|
|
|
总计 |
|
|
|
(1)根据表中的数据,能否在犯错误的概率不超过![]() 的前提下,认为电子产品的态度与年龄有关系?
的前提下,认为电子产品的态度与年龄有关系?
(2)为了答谢参与问卷调查的人员,该公司对参与本次问卷调查的人员进行抽奖活动,奖金额以及发放的概率如下:
奖金额 |
|
|
|
概率 |
|
|
|
现在甲、乙两人参与了抽奖活动,记两人获得的奖金总金额为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参与公式: 
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【题目】某种大型医疗检查机器生产商,对一次性购买2台机器的客户,推出两种超过质保期后两年内的延保维修优惠方案:方案一:交纳延保金7000元,在延保的两年内可免费维修2次,超过2次每次收取维修费2000元;方案二:交纳延保金10000元,在延保的两年内可免费维修4次,超过4次每次收取维修费1000元.某医院准备一次性购买2台这种机器。现需决策在购买机器时应购买哪种延保方案,为此搜集并整理了50台这种机器超过质保期后延保两年内维修的次数,得下表:
维修次数 | 0 | 1 | 2 | 3 |
台数 | 5 | 10 | 20 | 15 |
以这50台机器维修次数的频率代替1台机器维修次数发生的概率,记X表示这2台机器超过质保期后延保的两年内共需维修的次数。
(1)求X的分布列;
(2)以所需延保金及维修费用的期望值为决策依据,医院选择哪种延保方案更合算?

