题目内容
市场营销人员对过去几年某商品的价格及销售数量的关系作数据分析发现有如下规律:该商品的价格每上涨x%(x>0),销售数量就减少kx%(其中k为正常数).目前该商品定价为每个a元,统计其销售数量为b个.
(1)当k= 时,该商品的价格上涨多少,才能使销售的总金额达到最大?
时,该商品的价格上涨多少,才能使销售的总金额达到最大?
(2)在适当的涨价过程中,求使销售总金额不断增加时k的取值范围.
(1)当k=
 时,该商品的价格上涨多少,才能使销售的总金额达到最大?
时,该商品的价格上涨多少,才能使销售的总金额达到最大?(2)在适当的涨价过程中,求使销售总金额不断增加时k的取值范围.
(1) 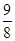 ab.(2) 0<k<1
ab.(2) 0<k<1
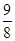 ab.(2) 0<k<1
ab.(2) 0<k<1由题意,价格上涨x%以后,销售总金额为y=a(1+x%)·b(1-kx%)= [-kx2+100(1-k)x+10000].
[-kx2+100(1-k)x+10000].
(1)当k= 时,y=
时,y= (-
(- x2+50x+10000)=
x2+50x+10000)= [22500-(x-50)2],
[22500-(x-50)2],
因此当x=50,即价格上涨50%时,y取最大值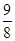 ab.
ab.
(2)y= [-kx2+100(1-k)x+10000],此二次函数的图象开口向下,对称轴为x=
[-kx2+100(1-k)x+10000],此二次函数的图象开口向下,对称轴为x= .
.
在适当涨价的过程中,销售总金额不断增加,即要求此函数当自变量x在{x|x>0}的一个子集内增大时,y也增大,因此 >0,解得0<k<1.
>0,解得0<k<1.
 [-kx2+100(1-k)x+10000].
[-kx2+100(1-k)x+10000].(1)当k=
 时,y=
时,y= (-
(- x2+50x+10000)=
x2+50x+10000)= [22500-(x-50)2],
[22500-(x-50)2],因此当x=50,即价格上涨50%时,y取最大值
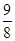 ab.
ab.(2)y=
 [-kx2+100(1-k)x+10000],此二次函数的图象开口向下,对称轴为x=
[-kx2+100(1-k)x+10000],此二次函数的图象开口向下,对称轴为x= .
.在适当涨价的过程中,销售总金额不断增加,即要求此函数当自变量x在{x|x>0}的一个子集内增大时,y也增大,因此
 >0,解得0<k<1.
>0,解得0<k<1.
练习册系列答案
相关题目
 ,证明数列{an}成等比数列,并求数列{xn}的通项公式.
,证明数列{an}成等比数列,并求数列{xn}的通项公式. ,
, ,沿对角线AC折成如图所示的四面体,二面角B-AC-D为
,沿对角线AC折成如图所示的四面体,二面角B-AC-D为 ,M为AC的中点,P在线段DM上,记DP=x,PA+PB=y,则函数y=f(x)的图象大致为( )
,M为AC的中点,P在线段DM上,记DP=x,PA+PB=y,则函数y=f(x)的图象大致为( )

 )图象上一动点,记m=
)图象上一动点,记m=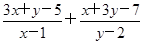 ,则当m最小时,点P的坐标为________.
,则当m最小时,点P的坐标为________.
 )x万元,假设所有桥墩都视为点且不考虑其他因素,记工程总费用为y万元.
)x万元,假设所有桥墩都视为点且不考虑其他因素,记工程总费用为y万元. ,x∈[-1,8],函数g(x)=ax+2,x∈[-1,8],若存在x∈[-1,8],使f(x)=g(x)成立,则实数a的取值范围是________.
,x∈[-1,8],函数g(x)=ax+2,x∈[-1,8],若存在x∈[-1,8],使f(x)=g(x)成立,则实数a的取值范围是________. 伴随函数”至少有一个零点.其中正确的结论个数是( )
伴随函数”至少有一个零点.其中正确的结论个数是( ) ,若
,若 ,
, ,则
,则 与
与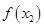 的大小关系为___________.
的大小关系为___________.