题目内容
已知函数f(x)＝x2－4，设曲线y＝f(x)在点(xn，f(xn))
处的切线与x轴的交点为(xn＋1,0)(n∈N＋)，其中x1为正实数．
(1)用xn表示xn＋1；
(2)求证：对一切正整数n，xn＋1≤xn的充要条件是x1≥2；
(3)若x1＝4，记an＝lg
，证明数列{an}成等比数列，并求数列{xn}的通项公式．
处的切线与x轴的交点为(xn＋1,0)(n∈N＋)，其中x1为正实数．
(1)用xn表示xn＋1；
(2)求证：对一切正整数n，xn＋1≤xn的充要条件是x1≥2；
(3)若x1＝4，记an＝lg
，证明数列{an}成等比数列，并求数列{xn}的通项公式．（1）xn＋1＝
（2）见解析（3）xn＝
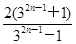
（2）见解析（3）xn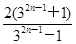＝(1)由题意可得f′(x)＝2x，
所以过曲线上点(xn，f(xn))的切线方程为
y－f(xn)＝f′(xn)(x－xn)，即y－(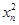
－4)＝2xn(x－xn)．
令y＝0，得－(－4)＝2xn(xn＋1－xn)．
即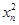＋4＝2xnxn＋1.显然xn≠0，∴xn＋1＝.
(2) (必要性)若对一切正整数n，有xn＋1≤xn，则x2≤x1，
即
≤x1，∴
≥4.而x1>0，即有x1≥2.
(充分性)若x1≥2>0，由xn＋1＝，
用数学归纳法易得xn>0，从而xn＋1＝≥2
＝2(n≥1)，
即xn≥2(n≥2)．又x1≥2，∴xn≥2(n≥1)．
于是xn＋1－xn＝－xn＝
＝
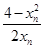≤0.?
即xn＋1≤xn对一切正整数n成立．
(3)xn＋1＝，知xn＋1＋2＝
，
同理，xn＋1－2＝
.故
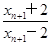＝()2.
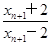从而lg＝2lg，即an＋1＝2an.所以，数列{an}成等比数列，
故an＝2n－1a1＝2n－1·lg
＝2n－1lg 3，
即lg＝2n－1lg 3.从而＝32n－1，所以xn＝.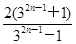
所以过曲线上点(xn，f(xn))的切线方程为
y－f(xn)＝f′(xn)(x－xn)，即y－(
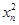－4)＝2xn(x－xn)．令y＝0，得－(
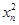－4)＝2xn(xn＋1－xn)．即
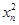＋4＝2xnxn＋1.显然xn≠0，∴xn＋1＝.(2) (必要性)若对一切正整数n，有xn＋1≤xn，则x2≤x1，
即
≤x1，∴≥4.而x1>0，即有x1≥2.(充分性)若x1≥2>0，由xn＋1＝
，用数学归纳法易得xn>0，从而xn＋1＝
≥2＝2(n≥1)，即xn≥2(n≥2)．又x1≥2，∴xn≥2(n≥1)．
于是xn＋1－xn＝
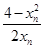－xn＝＝≤0.?即xn＋1≤xn对一切正整数n成立．
(3)xn＋1＝
，知xn＋1＋2＝，同理，xn＋1－2＝
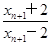.故＝()2. 从而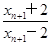lg
＝2lg，即an＋1＝2an.所以，数列{an}成等比数列，故an＝2n－1a1＝2n－1·lg
＝2n－1lg 3，即lg
＝2n－1lg 3.从而＝32n－1，所以xn＝.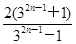
练习册系列答案
相关题目
,则
在
上的零点个数( )
时，该商品的价格上涨多少，才能使销售的总金额达到最大？
立方米，且l≥2r.假设该容器的建造费用仅与其表面积有关，已知圆柱形部分每平方米建造费用为3千元，半球形部分每平方米建造费用为c(c>3)千元．设该容器的建造费用为y千元．
,则s的最小值是 . 