题目内容
对于函数f(x),若存在区间A=[m,n],使得{y|y=f(x),x∈A}=A,则称函数f(x)为“和谐函数”,区间A为函数f(x)的一个“和谐区间”.给出下列4个函数:
①f(x)=sin(
x);
②f(x)=2x2-1;
③f(x)=|2x-1|;
④f(x)=ln(x+1).
其中存在唯一“和谐区间”的“和谐函数”为( )
①f(x)=sin(
| π |
| 2 |
②f(x)=2x2-1;
③f(x)=|2x-1|;
④f(x)=ln(x+1).
其中存在唯一“和谐区间”的“和谐函数”为( )
| A、①②③ | B、②③④ |
| C、①③ | D、②③ |
考点:元素与集合关系的判断
专题:函数的性质及应用,集合
分析:根据“和谐区间”的定义,我们要想说明函数存在“和谐区间”,我们只要举出一个符合定义的区间M即可,但要说明函数没有“和谐区间”,我们可以用反证明法来说明.由此对四个函数逐一进行判断,即可得到答案.
解答:解:①中,若f(x)=sin(
x)的周期是4,正弦函数的性质我们易得,A=[0,1]为函数的一个“和谐区间”;同时当A=[-1,0]时也是函数的一个“和谐区间”,∴不满足唯一性.
②中,若f(x)=2x2-1,当A=[-1,1]时,f(x)∈[-1,1],满足条件,且由二次函数的图象可知,满足条件的集合只有A=[-1,1]一个.∴f(x)=2x2-1满足题意.
③中,由幂函数的性质我们易得,M=[0,1]为函数f(x)=|2x-1|的“和谐区间”,由幂函数的图象可和,满足条件的集合只有A=[0,1]一个.∴f(x)=|2x-1|满足题意.
④中,∵f(x)=ln(x+1)单调递增,且函数的定义域为(-1,+∞),
若存在“和谐区间”,则满足
,即
,
∴m,n是方程ex-x-1=0的两个根,设f(x)=ex-x-1,f′(x)=ex-1,当x>0时,f′(x)>0,此时函数f(x)单调递增,当-1<x<0时,f′(x)<0,此时函数f(x)单调递减,
且f(0)=ex-x-1=0,故f(x)=2x-2x+2=0有且只有一个解,
故f(x)=ln(x+1)不存在“可等域区间”.
故存在唯一“和谐区间”的“和谐函数”为:②③.
故选:D
| π |
| 2 |
②中,若f(x)=2x2-1,当A=[-1,1]时,f(x)∈[-1,1],满足条件,且由二次函数的图象可知,满足条件的集合只有A=[-1,1]一个.∴f(x)=2x2-1满足题意.
③中,由幂函数的性质我们易得,M=[0,1]为函数f(x)=|2x-1|的“和谐区间”,由幂函数的图象可和,满足条件的集合只有A=[0,1]一个.∴f(x)=|2x-1|满足题意.
④中,∵f(x)=ln(x+1)单调递增,且函数的定义域为(-1,+∞),
若存在“和谐区间”,则满足
|
|
∴m,n是方程ex-x-1=0的两个根,设f(x)=ex-x-1,f′(x)=ex-1,当x>0时,f′(x)>0,此时函数f(x)单调递增,当-1<x<0时,f′(x)<0,此时函数f(x)单调递减,
且f(0)=ex-x-1=0,故f(x)=2x-2x+2=0有且只有一个解,
故f(x)=ln(x+1)不存在“可等域区间”.
故存在唯一“和谐区间”的“和谐函数”为:②③.
故选:D
点评:本题考查的知识点是函数的概念及其构造要求,在说明一个函数没有“和谐区间”时,利用函数的性质、图象结合反证法证明是解答本题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
设集合A={(x1,x2,x3,x4,x5)|xi∈{-1,0,1},i={1,2,3,4,5},那么集合A中满足条件“1≤|x1|+|x2|+|x3|+|x4|+|x5|≤3”的元素个数为( )
| A、60 | B、90 | C、120 | D、130 |
已知集合A={x∈Q|x>-1},B={x∈R|x<2},则下列说法正确的是( )
A、
| ||
| B、A∩B=(-1,2) | ||
| C、A∪B=R | ||
| D、1∈A∩B |
下列集合中不同于另外三个集合的是( )
| A、{x|x=1} | B、{x|x-1=0} | C、{x=1} | D、{1} |
 对应变换下变为点B(1,2),求M-1.
对应变换下变为点B(1,2),求M-1. ,则
,则 .
.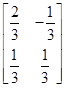 ,△ABC的顶点为A(0,0),B(2,0),C(1,2),求△ABC在矩阵M-1的变换作用下所得△A′B′C′的面积.
,△ABC的顶点为A(0,0),B(2,0),C(1,2),求△ABC在矩阵M-1的变换作用下所得△A′B′C′的面积.