题目内容
已知集合A={x∈Q|x＞-1}，B={x∈R|x＜2}，则下列说法正确的是（ ）
A、
| ||
| B、A∩B=（-1，2） | ||
| C、A∪B=R | ||
| D、1∈A∩B |
考点：元素与集合关系的判断
专题：集合
分析：先弄清楚集合A、B中元素的属性，然后根据相关概念对四个选项作出判断．
解答：解：由已知得，A表示大于-1的有理数集，B表示小于2的实数集，所以1∈A且1∈B，所以1∈A∩B．
故选D
故选D
点评：把每个集合中元素的属性弄清楚是解决此类集合问题的前提．
练习册系列答案
相关题目
对于函数f（x），若存在区间A=[m，n]，使得{y|y=f（x），x∈A}=A，则称函数f（x）为“和谐函数”，区间A为函数f（x）的一个“和谐区间”．给出下列4个函数：
①f（x）=sin（
x）；
②f（x）=2x2-1；
③f（x）=|2x-1|；
④f（x）=ln（x+1）．
其中存在唯一“和谐区间”的“和谐函数”为（ ）
①f（x）=sin（
| π |
| 2 |
②f（x）=2x2-1；
③f（x）=|2x-1|；
④f（x）=ln（x+1）．
其中存在唯一“和谐区间”的“和谐函数”为（ ）
| A、①②③ | B、②③④ |
| C、①③ | D、②③ |
设数集M同时满足条件①M中不含元素-1，0，1，②若a∈M，则
∈M．则下列结论正确的是（ ）
| 1+a |
| 1-a |
| A、集合M中至多有2个元素 |
| B、集合M中至多有3个元素 |
| C、集合M中有且仅有4个元素 |
| D、集合M中有无穷多个元素 |
集合{x∈N|x＜5}的另一种表示法是（ ）
| A、{1，2，3，4} | B、{0，1，2，3，4} | C、{1，2，3，4，5} | D、{0，1，2，3，4，5} |
设集合M={x|x＜2014}，N={x|0＜x＜1}，则下列关系中正确的是（ ）
| A、M∪N=R | B、M∩N={x|0＜x＜1} | C、N∈M | D、M∩N=∅ |
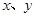的方程组：
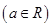，并对解的情况进行讨论．
，向量β＝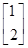
.求向量α，使得A2α＝β.
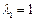及对应的一个特征向量
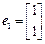和特征值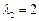
及对应的一个特征向量
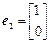，试求矩阵A．