题目内容

6．6件产品中有4件正品，2件次品，从中任取3件，则恰好有一件次品的概率为$\frac{3}{5}$．（结果用最简分数表示）

分析 6件产品中有4件正品，2件次品，先求出从中任取3件的基本事件总，再求出恰好有一件次品包含的基本事件个数，由此利用等可能事件概率计算公式能求出恰好有一件次品的概率．

解答 解：6件产品中有4件正品，2件次品，从中任取3件，基本事件总数n=${C}_{6}^{3}$=20，
恰好有一件次品包含的基本事件个数m=${C}_{4}^{2}{C}_{2}^{1}$=12，
∴恰好有一件次品的概率p=$\frac{m}{n}$=$\frac{12}{20}$=$\frac{3}{5}$．
故答案为：$\frac{3}{5}$．

点评 本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．

练习册系列答案
相关题目
14．设集合M是实数集R的一个子集，如果点x0∈R，满足：对任意?＞0，都存在x∈M，使得0＜|x-x0|＜?，称x0为集合M的一个“聚点”，若有集合：①有理数；②{cos$\frac{π}{n+1}$|n∈N*}；③{sin$\frac{π}{n+1}$|n∈N*}；④{$\frac{n}{n+1}$|n∈N*}．
其中以0为“聚点”的集合是①③．（写出所有符合题意的结论序号）
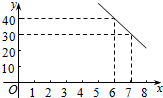17．某公司试销一种成本单价为50元/件的新产品，规定试销时销售单价不低于成本单价，又不高于80元/件．经试销调查，发现销售量y（件）与销售单价x（元/件）可近似看作一次函数y=kx+b的关系（如图所示）．
（1）根据图象，求一次函数y=kx+b的解析式．
（2）设公司获得的利润为S元（利润=销售总价-成本总价；销售总价=销售单价×销售量，成本总价=成本单价×销售量）．
①试用销售单价x表示利润S；
②试问销售单价定为多少时，该公司可获得最大利润？最大利润是多少？此时的销售量是多少？
14．若（1-2x）7=a0+a1x+a2x2+…+a7x7，则a0+a1+…+a7=-1．
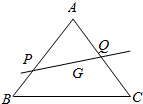1．如图，设G为△ABC的重心，过G的直线l分别交AB，AC于P，Q，若$\overrightarrow{AP}$=m$\overrightarrow{AB}$，$\overrightarrow{AQ}$=n$\overrightarrow{AC}$，令$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$
（1）试用$\overrightarrow a$，$\overrightarrow b$表示$\overrightarrow{AG}$；     
（2）求证：$\frac{1}{m}$+$\frac{1}{n}$=3．
11．已知a＞b＞c，且（a-c）（$\frac{1}{a-b}$+$\frac{4}{b-c}$）≥k恒成立，则k的取值范围是k≤9．
18．已知命题p：方程（ax+2）（ax-1）=0在[-1，1]上有解； 命题q：x1，x2是方程x2-mx-2=0的两个实根，不等式a2-5a-3≥|x1-x2|对任意实数m∈[-1，1]恒成立．若命题p是真命题，命题q为假命题，求实数a的取值范围．
15．已知函数f（x）=$\frac{1}{3}$x3+$\frac{1-a}{2}$x2-ax-a（a＞0，x∈R）
（I）求函数f（x）的单调区间；
（II）设函数f（x）在区间[0，3]上的最大值为M（t），最小值为m（t），记g（t）=M（t）-m（t）；求函数g（t）的解析式．
16．已知i为虚数单位，若复数z满足z•（-i）=2015+2016i，则$\overline{z}$为（　　）
A．2015+2016iB．2015-2016iC．-2016+2015iD．-2016-2015i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网