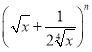题目内容
【题目】已知直三棱柱
中的底面为等腰直角三角形，
，点
分别是边
，
上动点，若直线
平面
，点
为线段
的中点，则点的轨迹为
A. 双曲线的一支一部分 B. 圆弧一部分
C. 线段去掉一个端点 D. 抛物线的一部分
【答案】C
【解析】
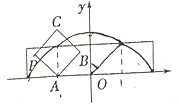
画出图形，利用直线与平面平行以及垂直关系，然后得出Q点的轨迹为线段．
如图作平面PQRK∥平面BCC1B1，可得到点M，N为平面PQRK与边
，
的交点，
取MN的中点D，由对称性可知，在梯形NQRM中，D到底面ABC的距离DF始终为三棱柱高的一半，故Q落在到底面ABC距离为三棱柱高的一半的平面上，且与底面ABC平行.
又D在底面的投影F始终在底面BC的高线AE上，即Q落在过底面BC的高线且与底面垂直的平面上，
所以Q在两个面的交线上，又只能落在柱体内，故为线段OH，又直线
平面
，所以去掉O点，故选C.
【题目】某调查机构对某校学生做了一个是否同意生“二孩”抽样调查，该调查机构从该校随机抽查了100名不同性别的学生，调查统计他们是同意父母生“二孩”还是反对父母生“二孩”，现已得知100人中同意父母生“二孩”占60%，统计情况如下表：
同意 | 不同意 | 合计 | |
男生 | a | 5 | |
女生 | 40 | d | |
合计 | 100 |
（1）求 a，d 的值，根据以上数据，能否有97.5%的把握认为是否同意父母生“二孩”与性别有关?请说明理由；
（2）将上述调查所得的频率视为概率，现在从所有学生中，采用随机抽样的方法抽取4 位学生进行长期跟踪调查，记被抽取的4位学生中持“同意”态度的人数为 X，求 X 的分布列及数学期望.
附：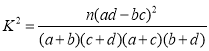
| 0.15 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】在2016年8月巴西里约热内卢举办的第31届奥运会上，乒乓球比赛团体决赛实行五场三胜制，且任何一方获胜三场比赛即结束.甲、乙两个代表队最终进入决赛，根据双方排定的出场顺序及以往战绩统计分析，甲队依次派出的五位选手分别战胜对手的概率如下表：
出场顺序 | 1号 | 2号 | 3号 | 4号 | 5号 |
获胜概率 |
|
|
|
|
|
若甲队横扫对手获胜（即3∶0获胜）的概率是
，比赛至少打满4场的概率为
.
（1）求
，
的值；
（2）求甲队获胜场数的分布列和数学期望.
