题目内容
已知圆 :
: ,圆
,圆 :
:
 ,过圆
,过圆 上任意一点
上任意一点 作圆
作圆 的两条切线
的两条切线 、
、 ,切点分别为
,切点分别为 、
、 ,则
,则 的最小值是( )
的最小值是( )
| A.5 | B.6 | C.10 | D.12 |
B
解析试题分析:(x-2)2+y2=4的圆心C(2,0),半径等于2,圆M (x-2-5cosθ)2+(y-5sinθ)2=1,
圆心M(2+5cosθ,5sinθ),半径等于1.
∵|CM|=5>2+1,故两圆相离.
∵ =
=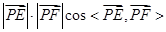 ,要使
,要使  最小,需
最小,需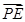 和
和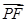 最小,且∠EPF 最大,
最小,且∠EPF 最大,
如图所示,设直线CM 和圆M交于H、G两点,则 最小值是
最小值是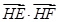 .
.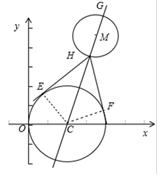
|H C|=|CM|-1=5-1=4,|H E|=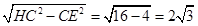 ,sin∠CHE=
,sin∠CHE=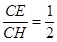 ,
,
∴cos∠EHF=cos2∠CHE=1-2sin2∠CHE=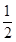 ,
,
∴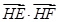 =
=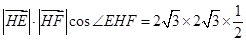 =6,故选B.
=6,故选B.
考点:1.圆的参数方程;2.平面向量数量积的运算;3.圆与圆的位置关系及其判定.

练习册系列答案
相关题目
圆 与圆
与圆 的位置关系为( )
的位置关系为( )
| A.内切 | B.相交 | C.外切 | D.相离 |
已知抛物线 的准线与圆
的准线与圆 相切,则
相切,则 的值为( )
的值为( )
A. | B. | C. | D. |
曲线 关于( )
关于( )
A.直线 对称 对称 | B.直线 对称 对称 |
C.直线 对称 对称 | D.直线 对称 对称 |
若 为圆
为圆 的弦
的弦 的中点,则直线
的中点,则直线 的方程是( )
的方程是( )
A. | B. |
C. | D. |
若圆 与圆
与圆 ,则
,则 ( )
( )
| A.21 | B.19 | C.9 | D.-11 |
直线 与圆
与圆 的位置关系是( )
的位置关系是( )
| A.相交 | B.相切 | C.相离 | D.无法确定 |
 与圆
与圆 相交于
相交于 两点,则
两点,则 是“
是“ 的面积为
的面积为 ”的( )
”的( ) 充分而不必要条件
充分而不必要条件  必要而不充分条件
必要而不充分条件  充分必要条件
充分必要条件  既不充分又不必要条件
既不充分又不必要条件


