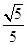题目内容
曲线
关于（ ）
A．直线 对称 | B．直线 对称 |
C．直线 对称 | D．直线 对称 |
B
解析试题分析：曲线是圆，将其化为标准形式：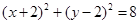
，圆心是
故关于
.
考点：圆的对称性.
练习册系列答案
相关题目
圆
的圆心和半径分别（ ）
A． | B． | C． | D． |
已知圆
：
，圆
：
，过圆上任意一点
作圆的两条切线
、
，切点分别为
、
，则
的最小值是（ ）
| A．5 | B．6 | C．10 | D．12 |
已知直线
与圆
交于
、
两点，
是原点，C是圆上一点，若
，则
的值为( )
A． | B． | C． | D． |
[2012·辽宁高考]将圆x2＋y2－2x－4y＋1＝0平分的直线是( )
| A．x＋y－1＝0 | B．x＋y＋3＝0 |
| C．x－y＋1＝0 | D．x－y＋3＝0 |
（2013•重庆）已知圆C1：（x﹣2）2+（y﹣3）2=1，圆C2：（x﹣3）2+（y﹣4）2=9，M，N分别是圆C1，C2上的动点，P为x轴上的动点，则|PM|+|PN|的最小值为（ ）
A．5 ﹣4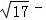 | B． 1 | C．6﹣2 | D． |
已知点M(a,b)在圆
外, 则直线ax + by = 1与圆O的位置关系是
| A．相切 | B．相交 | C．相离 | D．不确定 |
点P(4，－2)与圆x2＋y2＝4上任一点连线的中点轨迹方程是( )
| A．(x－2)2＋(y－1)2＝1 |
| B．(x＋2)2＋(y－1)2＝1 |
| C．(x－2)2＋(y＋1)2＝1 |
| D．(x－1)2＋(y＋2)2＝1 |