题目内容
(3分)(2011•重庆)在圆x2+y2﹣2x﹣6y=0内,过点E(0,1)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为( )
A. | B. | C. | D. |
B
解析试题分析:把圆的方程化为标准方程后,找出圆心坐标与圆的半径,根据图形可知,过点E最长的弦为直径AC,最短的弦为过E与直径AC垂直的弦BD,根据两点间的距离公式求出ME的长度,根据垂径定理得到E为BD的中点,在直角三角形BME中,根据勾股定理求出BE,则BD=2BE,然后利用AC与BD的乘积的一半即可求出四边形ABCD的面积.
解:把圆的方程化为标准方程得:(x﹣1)2+(y﹣3)2=10,
则圆心坐标为(1,3),半径为 ,
,
根据题意画出图象,如图所示:
由图象可知:过点E最长的弦为直径AC,最短的弦为过E与直径AC垂直的弦,则AC=2 ,MB=
,MB= ,ME=
,ME= =
=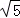 ,
,
所以BD=2BE=2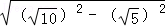 =2
=2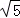 ,又AC⊥BD,
,又AC⊥BD,
所以四边形ABCD的面积S= AC•BD=
AC•BD= ×2
×2 ×2
×2 =10
=10 .
.
故选B
点评:此题考查学生掌握垂径定理及勾股定理的应用,灵活运用两点间的距离公式化简求值,是一道中档题.学生做题时注意对角线垂直的四边形的面积等于对角线乘积的一半.

圆 与直线
与直线 相切,正实数b的值为 ( )
相切,正实数b的值为 ( )
A. | B. | C. | D.3 |
已知圆 :
: ,圆
,圆 :
:
 ,过圆
,过圆 上任意一点
上任意一点 作圆
作圆 的两条切线
的两条切线 、
、 ,切点分别为
,切点分别为 、
、 ,则
,则 的最小值是( )
的最小值是( )
| A.5 | B.6 | C.10 | D.12 |
已知动圆 与圆
与圆 和圆
和圆 都外切,则动圆圆心
都外切,则动圆圆心 的轨迹是( )
的轨迹是( )
| A.圆 | B.椭圆 | C.双曲线 | D.双曲线的一支 |
过点M(1,2)的直线l将圆(x-2)2+y2=9分成两段弧,当其中的劣弧最短时,直线的方程是( )
| A.x=1 | B.y=1 |
| C.x-y+1=0 | D.x-2y+3=0 |
已知圆C的方程为 ,若以直线
,若以直线 上任意一点为圆心,以l为半径的圆与圆C没有公共点,则k的整数值是( )
上任意一点为圆心,以l为半径的圆与圆C没有公共点,则k的整数值是( )
A.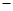 l l | B.0 | C.1 | D.2 |
(2013•重庆)已知圆C1:(x﹣2)2+(y﹣3)2=1,圆C2:(x﹣3)2+(y﹣4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为( )
A.5 ﹣4 ﹣4 | B.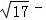 1 1 | C.6﹣2 | D. |
圆x2+y2+2x=0和x2+y2﹣4y=0的公共弦的长度为( )
A.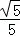 | B. | C. | D. |
 和圆:
和圆: 交于A、B两点,则AB的垂直平分线的方程是( ).
交于A、B两点,则AB的垂直平分线的方程是( ). B.
B. C.
C.  D.
D.