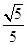题目内容
已知抛物线
的准线与圆
相切，则
的值为（ ）
A． | B． | C． | D． |
C
解析试题分析：抛物线的准线方程为
，圆心坐标为
，因此有
，解得
，故选C.
考点：1.抛物线的几何性质；2.直线与圆的位置关系
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
若圆C:
关于直线
对称，则由点
向圆所作的切线长的最小值是（ ）
| A．2 | B．4 | C．3 | D．6 |
已知圆
：
，圆
：
，过圆上任意一点
作圆的两条切线
、
，切点分别为
、
，则
的最小值是（ ）
| A．5 | B．6 | C．10 | D．12 |
已知
，则直线
与圆：
的位置关系是( )．
| A．相交 | B．相切 | C．相离 | D．不能确定 |
已知圆C：x2＋(y－3)2＝4，过A(－1,0)的直线l与圆C相交于P，Q两点，若|PQ|＝2
，则直线l的方程为( )
| A．x＝－1或4x＋3y－4＝0 |
| B．x＝－1或4x－3y＋4＝0 |
| C．x＝1或4x－3y＋4＝0 |
| D．x＝1或4x＋3y－4＝0 |
若圆O：x2＋y2＝4与圆C：x2＋y2＋4x－4y＋4＝0关于直线l对称，则直线l的方程是( )
| A．x＋y＝0 | B．x－y＝0 |
| C．x－y＋2＝0 | D．x＋y＋2＝0 |
[2012·辽宁高考]将圆x2＋y2－2x－4y＋1＝0平分的直线是( )
| A．x＋y－1＝0 | B．x＋y＋3＝0 |
| C．x－y＋1＝0 | D．x－y＋3＝0 |
已知点M(a,b)在圆
外, 则直线ax + by = 1与圆O的位置关系是
| A．相切 | B．相交 | C．相离 | D．不确定 |