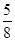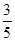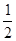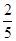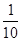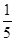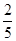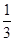题目内容
有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表:
已知在全部的105人中随机抽取1人为优秀的概率为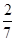
(Ⅰ)请完成上面的列联表;
(Ⅱ)从105名学生中选出10名学生组成参观团,若采用下面的方法选取:用简单随机抽样从105人中剔除5人,剩下的100人再按系统抽样的方法抽取10人,请写出在105人中,每人入选的概率(不必写过程);
(Ⅲ)把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号,试求抽到6号或10号的概率.
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合计 | | | 105 |
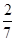
(Ⅰ)请完成上面的列联表;
(Ⅱ)从105名学生中选出10名学生组成参观团,若采用下面的方法选取:用简单随机抽样从105人中剔除5人,剩下的100人再按系统抽样的方法抽取10人,请写出在105人中,每人入选的概率(不必写过程);
(Ⅲ)把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号,试求抽到6号或10号的概率.
(Ⅰ)列联表见下面答案;(Ⅱ)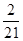 ;(Ⅲ)
;(Ⅲ)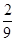 .
.
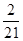 ;(Ⅲ)
;(Ⅲ)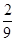 .
.试题分析:(Ⅰ)利用“在全部的105人中随机抽取1人为优秀的概率为
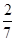 ”求出在105人中优秀的总人数为30人,从而就可以填出列联表中所有的数;(Ⅱ)直接写出概率(Ⅲ)先写出先后两次抛掷一枚均匀的骰子,出现的点数为
”求出在105人中优秀的总人数为30人,从而就可以填出列联表中所有的数;(Ⅱ)直接写出概率(Ⅲ)先写出先后两次抛掷一枚均匀的骰子,出现的点数为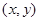 的所有情况,共36种,再写出“抽到6或10”的事件的所有情况共8种,所以概率为
的所有情况,共36种,再写出“抽到6或10”的事件的所有情况共8种,所以概率为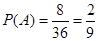 .
.试题解析:(Ⅰ)从
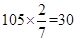 可知两个班的优秀生共30人,
可知两个班的优秀生共30人,| | 优秀 | 非优秀 | 总计 |
| 甲班 | 10 | 45 | 55 |
| 乙班 | 20 | 30 | 50 |
| 合计 | 30 | 75 | 105 |
(Ⅱ)
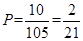 6分
6分(Ⅲ)设“抽到6或10”为事件
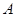 ,先后两次抛掷一枚均匀的骰子,出现的点数为
,先后两次抛掷一枚均匀的骰子,出现的点数为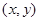 .所有的基本事件有
.所有的基本事件有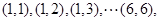 共36个.事件
共36个.事件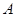 包含的基本事件有:
包含的基本事件有: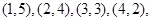
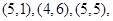
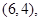 共8个,∴
共8个,∴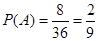
故抽到6号或10号的概率为
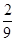 . 12分
. 12分
练习册系列答案
相关题目
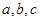 的值;
的值;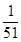
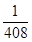
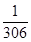

 ,第二次出现的点数记为
,第二次出现的点数记为 ,方程组
,方程组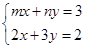 只有一组解的概率是( )
只有一组解的概率是( )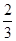

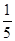

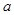 ,第二次朝上一面的点数为
,第二次朝上一面的点数为 ,则函数
,则函数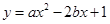 在
在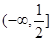 上为减函数的概率是 ( )
上为减函数的概率是 ( )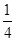
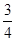


 ,再由乙猜甲刚才所想的数字,把乙猜的数字记为
,再由乙猜甲刚才所想的数字,把乙猜的数字记为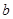 ,且
,且 。若
。若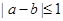 ,则称甲乙“心有灵犀”。现任意找两人玩这个游戏,得出他们“心有灵犀”的概率为 ( )
,则称甲乙“心有灵犀”。现任意找两人玩这个游戏,得出他们“心有灵犀”的概率为 ( )