题目内容
2.已知三点A(-1,0),B(1,0),C(-1,$\frac{3}{2}$)以A,B为焦点的椭圆经过C点.(1)求椭圆的标准方程;
(2)设点D(0,1),是否存在不平行x轴的直线l与椭圆交于不同的两点M,N的值,使得($\overrightarrow{DM}$+$\overrightarrow{DN}$)•$\overrightarrow{MN}$=0?若存在,求出直线l斜率的取值范围,若不存在,请说明理由.
分析 (1)通过设椭圆方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),利用以A,B为焦点的椭圆进过C点,计算即得结论;
(2)利用($\overrightarrow{DM}$+$\overrightarrow{DN}$)•$\overrightarrow{MN}$=0等价于|$\overrightarrow{DM}$|=|$\overrightarrow{DN}$|可设直线l:y=kx+m(k≠0),一方面通过联立直线l与椭圆方程并令△>0可知4k2+3>m2,另一方面利用中点坐标公式及$\frac{{y}_{0}-1}{{x}_{0}}$=-$\frac{1}{k}$计算可知m=-3-4k2,由此得出两者矛盾,进而可得结论.
解答 解:(1)依题意,设椭圆方程为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),则
$\left\{\begin{array}{l}{\frac{(-1)^{2}}{{a}^{2}}+\frac{(\frac{3}{2})^{2}}{{b}^{2}}=1}\\{{a}^{2}-{b}^{2}=1}\end{array}\right.$,
解得:a2=4,b2=3,
∴椭圆的标准方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)结论:不存在不平行x轴的直线l与椭圆交于不同的两点M,N的值,使得($\overrightarrow{DM}$+$\overrightarrow{DN}$)•$\overrightarrow{MN}$=0.
理由如下:
∵($\overrightarrow{DM}$+$\overrightarrow{DN}$)•$\overrightarrow{MN}$=0等价于|$\overrightarrow{DM}$|=|$\overrightarrow{DN}$|,
∴若存在符合条件的直线,则该直线的斜率一定存在,否则与点D(0,1)在x轴上矛盾,
∴可设直线l:y=kx+m(k≠0),并与椭圆方程联立,
整理得:(4k2+3)x2+8kmx+4m2-12=0,
令△=64k2m2-4(4k2+3)(4m2-12)>0,
化简得:4k2+3>m2,
设M(x1,y1)、N(x2,y2),MN的中点为Q(x0,y0),
∴x0=$\frac{1}{2}$(x1+x2)=-$\frac{4km}{4{k}^{2}+3}$,y0=kx0+m=$\frac{3m}{4{k}^{2}+3}$,
又∵|$\overrightarrow{DM}$|=|$\overrightarrow{DN}$|,
∴$\frac{{y}_{0}-1}{{x}_{0}}$=-$\frac{1}{k}$,即$\frac{\frac{3m}{4{k}^{2}+3}-1}{-\frac{3m}{4{k}^{2}+3}}$=-$\frac{1}{k}$,
解得:m=-3-4k2,
又∵4k2+3>m2,
∴4k2+3>(4k2+3)2,
而这是不可能的,即满足条件的直线l不存在.
点评 本题是一道关于直线与圆锥曲线的综合题,注意解题方法的积累,属于中档题.

| A. | -1 | B. | -2 | C. | -3 | D. | 1 |
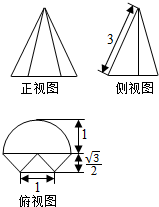 一个几何体的三视图如图所示,其俯视图为一个半圆和一个等腰梯形,则该几何体的体积为( )
一个几何体的三视图如图所示,其俯视图为一个半圆和一个等腰梯形,则该几何体的体积为( )| A. | $\frac{\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{4}$ | B. | $\frac{\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{2}$ | C. | $\frac{2\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{4}$ | D. | $\frac{2\sqrt{2}}{3}$π+$\frac{\sqrt{6}}{2}$ |
| A. | 6 | B. | 12 | C. | 24 | D. | 3 |