题目内容
已知x,y满足0≤x≤
,则
的取值范围是
| 4-y2 |
| y-2 |
| x-3 |
[0,
]
| 12 |
| 5 |
[0,
]
.| 12 |
| 5 |
分析:借助已知动点在半圆上任意动,而所求式子形式可以联想成在半圆上动点M与定点N(3,2)连线的斜率,求得过点N的切线的斜率,数形结合进而求解.
解答: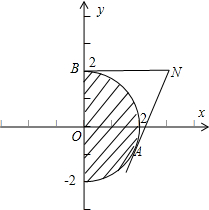 解:由 x,y满足0≤x≤
解:由 x,y满足0≤x≤
,
可得 x2+y2≤4,x≥0.
故满足条件的点(x,y)在半圆:x2+y2≤4 (x≥0)是如图所示的半圆面:
而
表示半圆上的点M(x,y)与点 N(3,2)
连线的斜率k,
显然k存在.
设半圆的切线方程为 y-2=k(x-3),即 kx-y+2-3k=0,
则由圆心O(0,0)到切线的距离等于半径可得
=r=2,
求得k=0,或 k=
,
数形结合可得k的范围为[0,
],
故答案为[0,
].
 解:由 x,y满足0≤x≤
解:由 x,y满足0≤x≤| 4-y2 |
可得 x2+y2≤4,x≥0.
故满足条件的点(x,y)在半圆:x2+y2≤4 (x≥0)是如图所示的半圆面:
而
| y-2 |
| x-3 |
连线的斜率k,
显然k存在.
设半圆的切线方程为 y-2=k(x-3),即 kx-y+2-3k=0,
则由圆心O(0,0)到切线的距离等于半径可得
| |2-3k| | ||
|
求得k=0,或 k=
| 12 |
| 5 |
数形结合可得k的范围为[0,
| 12 |
| 5 |
故答案为[0,
| 12 |
| 5 |
点评:此题重点考查了斜率公式,及直线与圆的相切与相交的关系,还考查了利用几何思想解决代数式子的等价转化、数形结合的思想,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目