题目内容
【题目】已知复数z=（a2﹣7a+6）+（a2﹣5a﹣6）i（a∈R）
（1）若复数z为纯虚数，求实数a的值；
（2）若复数z在复平面内的对应点在第四象限，求实数a的取值范围．
【答案】
（1）解：若复数z=（a2﹣7a+6）+（a2﹣5a﹣6）i（a∈R）为纯虚数，
则 
，
解得：a=1
（2）解：若复数z在复平面内的对应点在第四象限，
则 
，
解①得：a＜1或a＞6，
解②得﹣1＜a＜6．
取交集得：﹣1＜a＜1．
∴实数a的取值范围是（﹣1，1）
【解析】（1）由实部等于0且虚部不为0联立不等式组求解；（2）由实部大于0且虚部小于0联立不等式组得答案．
【考点精析】利用复数的定义对题目进行判断即可得到答案，需要熟知形如
的数叫做复数，
和
分别叫它的实部和虚部．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
【题目】已知某校5个学生的数学和物理成绩如表
学生的编号i | 1 | 2 | 3 | 4 | 5 |
数学xi | 80 | 75 | 70 | 65 | 60 |
物理yi | 70 | 66 | 68 | 64 | 62 |
（Ⅰ）假设在对这5名学生成绩进行统计时，把这5名学生的物理成绩搞乱了，数学成绩没出现问题，问：恰有2名学生的物理成绩是自己的实际分数的概率是多少？
（Ⅱ）通过大量事实证明发现，一个学生的数学成绩和物理成绩具有很强的线性相关关系的，在上述表格是正确的前提下，用x表示数学成绩，用y表示物理成绩，求y与x的回归方程；
参考公式： 
= 
， 
．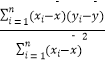