题目内容
【题目】已知圆
，某抛物线的顶点为原点
，焦点为圆心
，经过点
的直线
交圆
于
， 
两点，交此抛物线于
， 
两点，其中
， 
在第一象限， 
， 
在第二象限.
(1)求该抛物线的方程；
(2)是否存在直线
，使
是
与
的等差中项？若存在，求直线
的方程；若不存在，请说明理由.
【答案】（1）抛物线的方程为
（2）存在满足要求的直线
，其方程为
或
【解析】试题分析：（1）圆方程可化为可化为
圆心
的坐标为
， 
抛物线的方程为
；（2）由等差数列性质可得
，再由
， 
， 
存在满足要求的直线
，其方程为
或
.
试题解析：
（1）
可化为
，
根据已知抛物线的方程为
（
）.
∵圆心
的坐标为
，∴
，解得
.
∴抛物线的方程为
.
（2）∵
是
与
的等差中项，圆
的半径为2，∴
.
∴
.
由题知，直线
的斜率存在，故可设直线
的方程为
，
设
， 
，
由
，得
， 
，
故
， 
.
∵
∴
由
，解得
.
∴存在满足要求的直线
，其方程为
或
练习册系列答案
相关题目
【题目】某市的教育主管部门对所管辖的学校进行年终督导评估，为了解某学校师生对学校教学管理的满意度，分别从教师和不同年级的同学中随机抽取若干师生，进行评分(满分100分)，绘制如下频率分布直方图(分组区间为
， 
， 
， 
， 
， 
)，并将分数从低到高分为四个等级：
满意度评分 |
|
|
|
|
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
已知满意度等级为基本满意的有340人.
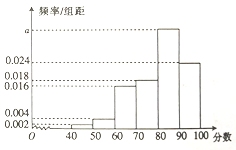
(1)求表中
的值及不满意的人数；
(2)在等级为不满意的师生中，老师占
，现从该等级师生中按分层抽样抽取12人了解不满意的原因，并从中抽取3人担任整改督导员，记
为老师整改督导员的人数，求
的分布列及数学期望.
