题目内容
已知椭圆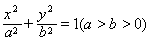 的左、右焦点分别为
的左、右焦点分别为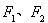 ,且
,且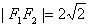 ,长轴的一个端点与短轴两个端点组成等边三角形的三个顶点.
,长轴的一个端点与短轴两个端点组成等边三角形的三个顶点.
(1)求椭圆方程;
(2)设椭圆与直线 相交于不同的两点M、N,又点
相交于不同的两点M、N,又点 ,当
,当 时,求实数m的取值范围,
时,求实数m的取值范围,
【答案】
(1)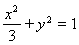 .
.
(2)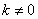 时,
时,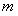 的取值范围是
的取值范围是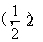 ;
;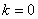 时,
时,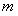 的取值范围是
的取值范围是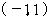
【解析】
试题分析:(1)由已知,可得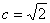 ,
,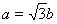 ,
,
利用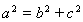 ,即得
,即得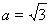 ,
,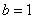 ,求得椭圆方程.
,求得椭圆方程.
(2)应注意讨论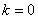 和
和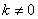 的两种情况.
的两种情况.
首先当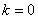 时,直线和椭圆有两交点只需
时,直线和椭圆有两交点只需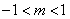 ;
;
当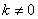 时,设弦
时,设弦 的中点为
的中点为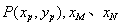 分别为点
分别为点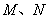 的横坐标,
的横坐标,
联立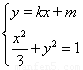 ,得
,得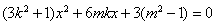 ,
,
注意根据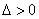 ,确定
,确定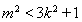 ① 平时解题时,易忽视这一点.
① 平时解题时,易忽视这一点.
应用韦达定理及中点坐标公式以及 得到
得到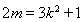 ②,
②,
将②代入①得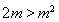 ,解得
,解得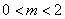 , 由②得
, 由②得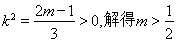 ,
,
故所求的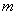 取值范围是
取值范围是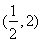 .
.
试题解析:(1)由已知,可得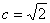 ,
,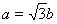 ,
,
∵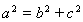 ,∴
,∴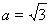 ,
,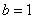 ,
,
∴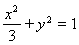 . 4分
. 4分
(2)当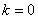 时,直线和椭圆有两交点只需
时,直线和椭圆有两交点只需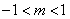 ; 5分
; 5分
当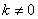 时,设弦
时,设弦 的中点为
的中点为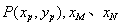 分别为点
分别为点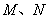 的横坐标,由
的横坐标,由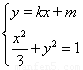 ,得
,得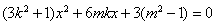 ,
,
由于直线与椭圆有两个不同的交点,所以
 ,即
,即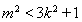 ① 7分
① 7分
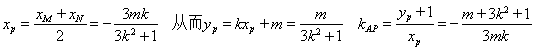 9分
9分
又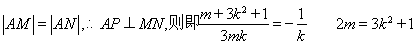 ②, 10分
②, 10分
将②代入①得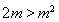 ,解得
,解得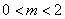 , 由②得
, 由②得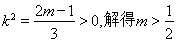 ,
,
故所求的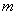 取值范围是
取值范围是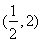 . 12分
. 12分
综上知,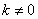 时,
时,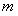 的取值范围是
的取值范围是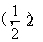 ;
;
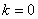 时,
时,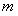 的取值范围是
的取值范围是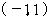 13分
13分
考点:椭圆的方程,直线与椭圆的位置关系,不等式解法.

练习册系列答案
相关题目
 的左、右焦点分别为
的左、右焦点分别为 ,
, ,
点
,
点 是椭圆的一个顶点,△
是椭圆的一个顶点,△ 是等腰直角三角形.
是等腰直角三角形. 分别作直线
分别作直线 ,
, 交椭圆于
交椭圆于 ,
, 两点,设两直线的斜率分别为
两点,设两直线的斜率分别为 ,
, ,且
,且 ,证明:直线
,证明:直线 过定点(
过定点( ).
). 的左、右焦点分别为F1、F2,其中
的左、右焦点分别为F1、F2,其中 的焦点,M是C1与C2在第一象限的交点,且
的焦点,M是C1与C2在第一象限的交点,且
 上,求直线AC的方程。
上,求直线AC的方程。 的左、右焦点分别为
的左、右焦点分别为 、
、 ,离心率
,离心率 ,右准线方程为
,右准线方程为 .
. 与该椭圆交于M、N两点,且
与该椭圆交于M、N两点,且 ,求直线
,求直线