题目内容
19.已知实数a,b,c满足$\frac{1}{4}$a2+$\frac{1}{4}$b2+c2=1,则ab+2bc+2ca的取值范围是( )| A. | (-∞,4] | B. | [-4,4] | C. | [-2,4] | D. | [-1,4] |
分析 把已知的等式变形,得到2a2+2b2+8c2=8,然后结合基本不等式求得ab+2bc+2ca≤4;再由($\frac{1}{2}$a+$\frac{1}{2}$b+c)2≥0,结合已知的等式求得ab+2bc+2ca≥-2.
解答 解:由$\frac{1}{4}$a2+$\frac{1}{4}$b2+c2=1,得a2+b2+4c2=4,即2a2+2b2+8c2=8.
∴8=2a2+2b2+8c2=(a2+b2)+(a2+4c2)+(b2+4c2)≥2ab+4ac+4bc.
∴ab+2bc+2ca≤4(当且仅当a=b=2c时取等号);
又$\frac{1}{4}$a2+$\frac{1}{4}$b2+c2+2($\frac{1}{4}$ab+$\frac{1}{2}$bc+$\frac{1}{2}$ca)=($\frac{1}{2}$a+$\frac{1}{2}$b+c)2≥0,
∴1+$\frac{1}{2}$(ab+2bc+2ca)≥0,
∴ab+2bc+2ca≥-2.
则ab+2bc+2ca的取值范围是[-2,4].
故选:C.
点评 本题考查基本不等式求最值,考查了灵活变形能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下列函数中,既是偶函数又存在零点的是( )
| A. | y=lnx | B. | y=x2+1 | C. | y=sinx | D. | y=cosx |
4.为了了解所加工一批零件的长度,抽测了其中200个零件的长度,在这个问题中,200个零件的长度是( )
| A. | 总体 | B. | 个体是每一个零件 | ||
| C. | 总体的一个样本 | D. | 样本容量 |
8.已知随机变量X的分布列如下:
(1)求m的值;
(2)求E(X);
(3)若Y=2X-3,求E(Y).
| X | -2 | -1 | 0 | 1 | 2 |
| P | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{5}$ | m | $\frac{1}{20}$ |
(2)求E(X);
(3)若Y=2X-3,求E(Y).
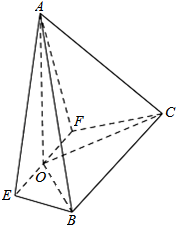 如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点.
如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点.