题目内容
2.已知动点P(x,y)满足$\left\{\begin{array}{l}{2x+y≤2}\\{x≥0}\\{(x+\sqrt{{x}^{2}+1})(y+\sqrt{{y}^{2}+1})≥1}\end{array}\right.$,则x2+y2+2y的最小值-$\frac{1}{2}$,此时x=$\frac{1}{2}$,y=$-\frac{1}{2}$.分析 不等式组中的第三个不等式可化为x+y≥0,作出该不等式组表示的平面区域,x2+y2+2y的几何意义为可行域内的动点到定点(0,-1)距离的平方减1,由此得答案.
解答 解:由(x+$\sqrt{{x}^{2}+1}$)(y+$\sqrt{{y}^{2}+1}$)≥1,
∵y+$\sqrt{{y}^{2}+1}$>y+$\sqrt{{y}^{2}}$=y+|y|≥0,
∴x+$\sqrt{{x}^{2}+1}$≥$\frac{1}{\sqrt{{y}^{2}+1}+y}=\sqrt{{y}^{2}+1}-y=\sqrt{(-y)^{2}+1}+(-y)$,
∵函数f(x)=x+$\sqrt{{x}^{2}+1}$是增函数,
∴x≥-y,即x+y≥0.
∴原不等式组化为$\left\{\begin{array}{l}{2x+y≤2}\\{x≥0}\\{x+y≥0}\end{array}\right.$.
该不等式组表示的平面区域如下图:
∵x2+y2+2y=${\sqrt{{x}^{2}+(y+1)^{2}}}^{2}-1$.
由点到直线的距离公式可得,P(0,-1)到直线x+y=0的距离为d=$\frac{|-1|}{\sqrt{2}}=\frac{\sqrt{2}}{2}$.
则x2+y2+2y的最小值为$\frac{1}{2}-1=-\frac{1}{2}$.
联立$\left\{\begin{array}{l}{x+y=0}\\{y=x-1}\end{array}\right.$,解得x=$\frac{1}{2}$,y=-$\frac{1}{2}$.
故答案为:$-\frac{1}{2}$,$\frac{1}{2}$,$-\frac{1}{2}$.
点评 本题考查不等式组表示的平面区域的概念,关键是把原不等式组转化,考查数形结合的解题思想方法,属于有一定难度问题.

| A. | 16 | B. | 36 | C. | 42 | D. | 60 |
| A. | -$\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | -$\frac{{\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |
| A. | $\frac{7}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{78}{71}$ |
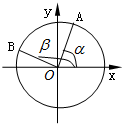 如图,在平面直角坐标系xoy中,以ox轴为始边作一个锐角α和一个钝角β,它们的终边分别与单位圆相交于点A和点B.且点A的坐标为$(\frac{{\sqrt{5}}}{5},\frac{{2\sqrt{5}}}{5})$,点B的坐标为$(-\frac{{3\sqrt{10}}}{10},\frac{{\sqrt{10}}}{10})$.
如图,在平面直角坐标系xoy中,以ox轴为始边作一个锐角α和一个钝角β,它们的终边分别与单位圆相交于点A和点B.且点A的坐标为$(\frac{{\sqrt{5}}}{5},\frac{{2\sqrt{5}}}{5})$,点B的坐标为$(-\frac{{3\sqrt{10}}}{10},\frac{{\sqrt{10}}}{10})$.