Question

12．在等腰△ABC中，已知sinA：sinB=1：2，底边BC=10，则△ABC的周长是50； 面积是25$\sqrt{15}$．

Answer 1

分析 由已知可得sinB=2sinA，由正弦定理解得b=c=20，可求周长，利用余弦定理先求cosA，即可求得sinA=$\sqrt{1-co{s}^{2}A}$的值，利用三角形面积公式即可得解．

解答 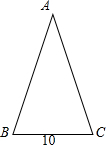解：∵sinA：sinB=1：2，可得：sinB=2sinA，
又∵在等腰△ABC中，底边BC=10，
∴由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}$可得：$\frac{10}{sinA}=\frac{b}{sinB}=\frac{b}{2sinA}$，解得b=c=20，
∴△ABC的周长l=a+b+c=10+20+20=50，
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{400+400-100}{2×20×20}$=$\frac{7}{8}$，sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{\sqrt{15}}{8}$，
面积S=$\frac{1}{2}$bcsinA=$\frac{1}{2}×20×20×$$\frac{\sqrt{15}}{8}$=25$\sqrt{15}$．
故答案为：50，25$\sqrt{15}$．

点评 本题主要考查了正弦定理，余弦定理，三角形面积公式，同角三角函数基本关系式的应用，熟练掌握公式及定理是解题的关键，属于基本知识的考查．